早教吧作业答案频道 -->数学-->
已知:如图,∠1=∠2,P为BN上的一点,PF⊥BC于F,PA=PC,(1)求证:∠PCB+∠BAP=180°;(2)线段BF、线段BC、线段AB之间有何数量关系?写出你的猜想及证明思路.
题目详情
已知:如图,∠1=∠2,P为BN上的一点,PF⊥BC于F,PA=PC,
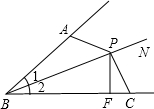
(1)求证:∠PCB+∠BAP=180°;
(2)线段BF、线段BC、线段AB之间有何数量关系?写出你的猜想及证明思路.

(1)求证:∠PCB+∠BAP=180°;
(2)线段BF、线段BC、线段AB之间有何数量关系?写出你的猜想及证明思路.
▼优质解答
答案和解析
(1)证明:过P点作PE⊥BA于点E,如图所示.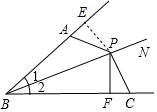
∵∠1=∠2,PF⊥BC,
∴PE=PF.
在Rt△PAE与Rt△PCF中,
,
∴Rt△PAE≌Rt△PCF(HL),
∴∠PCF=∠PAE.
∵∠PAE+∠BAP=180°,
∴∠PCB+∠BAP=180°.
(2) 2BF=AB+BC.
证明:∵Rt△PAE≌Rt△PCF,
∴AE=CF.
在Rt△PBE和Rt△PBF中,
,
∴Rt△PBE≌Rt△PBF(HL),
∴BE=BF.
∴2BF=BE+BF=AB+AE+BF=AB+FC+BF=AB+AC.

∵∠1=∠2,PF⊥BC,
∴PE=PF.
在Rt△PAE与Rt△PCF中,
|
∴Rt△PAE≌Rt△PCF(HL),
∴∠PCF=∠PAE.
∵∠PAE+∠BAP=180°,
∴∠PCB+∠BAP=180°.
(2) 2BF=AB+BC.
证明:∵Rt△PAE≌Rt△PCF,
∴AE=CF.
在Rt△PBE和Rt△PBF中,
|
∴Rt△PBE≌Rt△PBF(HL),
∴BE=BF.
∴2BF=BE+BF=AB+AE+BF=AB+FC+BF=AB+AC.
看了 已知:如图,∠1=∠2,P为...的网友还看了以下:
P(A/B)+P(A非/B非)=1证明AB独立我这样证:原始=P(A/B)+1-P(A/B非)=1 2020-04-06 …
概率论 P(B|A)+P(非B|非A)=1 求证A B 相互独立P(A),P(B)均大于0小于1, 2020-05-16 …
《展业证》的业务范围和销售区域以( )的业务范围和经营区域为限。A.所属保险公司经营许可证上B.保 2020-05-22 …
下列有关原始凭证的说法,正确的有()。A:不同内容和类别的原始凭证可以汇总填制在一张记账凭证上B: 2020-06-10 …
1,P(A)=0.4P(AB)=0.2P(A|B)+P(A非|B非)=1求P(A并B)2,证明若P 2020-06-14 …
设点A(x1,y1),B(x2,y2)在抛物线y^2=2px(p>0)上求证:直线AB在x轴上的截 2020-06-14 …
概率论与数理统计里的一道证明题设本题涉及的事件均有意义,设A,B都是事件.1.已知P(A)>0,证 2020-06-18 …
已知A,B是抛物线y2=2px(p>0)上的两点,且满足OA垂直OB.1:求证:A,B两点的横坐已 2020-07-01 …
1已知函数f(x)是R上的增函数,且a,b属于R.对于命题p:若a+b>=0,则f(a)+f(b)> 2020-11-30 …
求证若B⊂A,则P(A-B)=P(A)-P(B)且P(A)≥P(B)……谢谢……给出一种解法,但是需 2020-12-01 …