如图，一段抛物线y=-x2+4x（0≤x≤4），记为C1，它与x轴交于点O、A1；将C1绕点A1旋转180°得C2，交x轴于点A2；将C2绕点A2旋转180°得C3，交x轴于点A3…如此进行下去，直至得抛物线C2015．若点P

Question

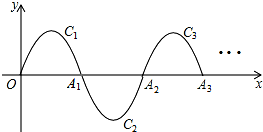
如图，一段抛物线y=-x²+4x（0≤x≤4），记为C₁，它与x轴交于点O、A₁；将C₁绕点A₁旋转180°得C₂，交x轴于点A₂；将C₂绕点A₂旋转180°得C₃，交x轴于点A₃…如此进行下去，直至得抛物线C₂₀₁₅．若点P（m，3）在第2015段抛物线C₂₀₁₅上，则m=___．

Answer 1

∵一段抛物线：y=-x（x-4）（0≤x≤4），
∴图象与x轴交点坐标为：（0，0），（4，0），
∴OA₁=4，
∵将C₁绕点A₁旋转180°得C₂，交x轴于点A₂；
∴OA₂=2×4=8，
同理可得OA₃=3×4=12，
…
∴OA₂₀₁₅=2014×4=8056，
∴第2015段抛物线C₂₀₁₅可看作第1段抛物线y=-x²+4x（0≤x≤4）向右平移8056个单位，
当y=3时，-x²+4x=3，解得x₁=1，x₂=3，
∴点（1，3）和点（3，3）向右平移8056个单位所得对应点的坐标为（8057，3），（8059，3），
∴m的值为8057或8059．
故答案为8057或8059．