早教吧作业答案频道 -->数学-->
探索研究:已知:△ABC和△CDE都是等边三角形.(1)如图1,若点A、C、E在一条直线上时,我们可以得到结论:线段AD与BE的数量关系为:,线段AD与BE所成的锐角度数为°;(2)如图2
题目详情
探索研究:已知:△ABC和△CDE都是等边三角形.
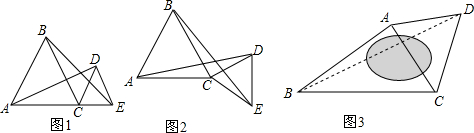
(1)如图1,若点A、C、E在一条直线上时,我们可以得到结论:线段AD与BE的数量关系为:___,
线段AD与BE所成的锐角度数为___°;
(2)如图2,当点A、C、E不在一条直线上时,请证明(1)中的结论仍然成立;
灵活运用:
如图3,某广场是一个四边形区域ABCD,现测得:AB=60m,BC=80m,且∠ABC=30°,∠DAC=∠DCA=60°,试求水池两旁B、D两点之间的距离.
(1)如图1,若点A、C、E在一条直线上时,我们可以得到结论:线段AD与BE的数量关系为:___,
线段AD与BE所成的锐角度数为___°;
(2)如图2,当点A、C、E不在一条直线上时,请证明(1)中的结论仍然成立;
灵活运用:
如图3,某广场是一个四边形区域ABCD,现测得:AB=60m,BC=80m,且∠ABC=30°,∠DAC=∠DCA=60°,试求水池两旁B、D两点之间的距离.

▼优质解答
答案和解析
(1)如图1,
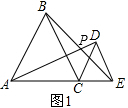
∵△ABC和△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠ADC=∠BEC,
由三角形的外角性质,∠DPE=∠PEA+∠DAC,
∠DCE=∠ADC+∠DAC,
∴∠DPE=∠DCE=60°;
故答案为:相等,60;
(2)如图2,
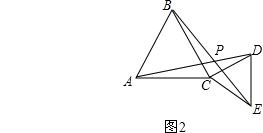
∵△ABC和△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE,
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠DAC=∠EBC,
∴∠BPA=180°-∠ABP-∠BAP=180°-∠ABC-∠BAC=60°.
(3)如图3,以AB为边在△ABC外侧作等边△ABE,连接CE.
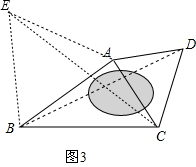
由(2)可得:BD=CE
∴∠EBC=60°+30°=90°,
∴△EBC是直角三角形
∵EB=60m BC=80m,
∴CE=
=
=100(m).
∴水池两旁B、D两点之间的距离为100m.

∵△ABC和△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE,
在△ACD和△BCE中,
|
∴△ACD≌△BCE(SAS),
∴AD=BE,∠ADC=∠BEC,
由三角形的外角性质,∠DPE=∠PEA+∠DAC,
∠DCE=∠ADC+∠DAC,
∴∠DPE=∠DCE=60°;
故答案为:相等,60;
(2)如图2,

∵△ABC和△CDE都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE,
在△ACD和△BCE中,
|
∴△ACD≌△BCE(SAS),
∴AD=BE,∠DAC=∠EBC,
∴∠BPA=180°-∠ABP-∠BAP=180°-∠ABC-∠BAC=60°.
(3)如图3,以AB为边在△ABC外侧作等边△ABE,连接CE.

由(2)可得:BD=CE
∴∠EBC=60°+30°=90°,
∴△EBC是直角三角形
∵EB=60m BC=80m,
∴CE=
| BE2+BC2 |
| 602+802 |
∴水池两旁B、D两点之间的距离为100m.
看了 探索研究:已知:△ABC和△...的网友还看了以下:
在三角形ABC中,如果有cosC小于0,则三角形一定是( )【那如果是大于0或者=0选什么】A.钝 2020-05-16 …
对于一个三角形设其三个内角的度数为X、Y、Z.若x、Y、Z满足X^2+Y^2=Z^2,我们定义这个 2020-06-12 …
下列说法不正确的是A.三角形的三个内角中,至少有一个钝角B.三角形的三个内角中,至少有一个内角不大 2020-06-26 …
下列说法不正确的是A.三角形的三个内角中,至少有一个钝角B.三角形的三个内角中,至少有一个内角不大 2020-06-26 …
下列词语中书写完全正确的一项是A、心无旁督鹜,趋之若鹜,目不暇接,遐想,B,一代天骄,矫揉造作,红 2020-06-26 …
列说法不正确的是A.tanA的值越大,梯子越陡B.山坡的坡度越大,山坡坡角的度数越大C.锐角的正切 2020-06-27 …
如题锐角△ABC中如图,锐角△ABC中,∠BAC=45°,两条高AD、CE相交于点F(1)求证:A 2020-07-22 …
如图,锐角△ABC中,BC=6,S△ABC=12,两动点M,N分别在边AB,AC上滑动且MN‖BC 2020-07-22 …
1.一个角的余角()A:一定是钝角B:一定是锐角C:锐角,钝角都有可能,但不可能是直角D:一上答案 2020-07-30 …
在一个三角形中,如果有两个锐角的和小于90°,那么这个三角形一定是()A.钝角三角形B.直角三角形 2020-08-03 …