早教吧作业答案频道 -->数学-->
在△OAB中,∠OAB=90°,∠AOB=30°,OB=4.以OB为边,在△OAB外作等边△OBC,E是OC上的一点.(1)如图1,当点E是OC的中点时,求证:四边形ABCE是平行四边形;(2)如图2,点F是BC上的一点,将四
题目详情
在△OAB中,∠OAB=90°,∠AOB=30°,OB=4.以OB为边,在△OAB外作等边△OBC,E是OC上的一点.
(1)如图1,当点E是OC的中点时,求证:四边形ABCE是平行四边形;
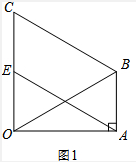
(2)如图2,点F是BC上的一点,将四边形ABCO折叠,使点C与点A重合,折痕为EF,求OE的长.
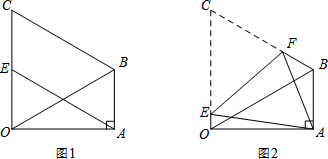
(1)如图1,当点E是OC的中点时,求证:四边形ABCE是平行四边形;
(2)如图2,点F是BC上的一点,将四边形ABCO折叠,使点C与点A重合,折痕为EF,求OE的长.

▼优质解答
答案和解析
(1)证明:如图1,∵△OBC为等边三角形,
 ∴OC=OB,∠COB=60°.,
∴OC=OB,∠COB=60°.,
∵点E是OC的中点,
∴EC=
OC=
OB,
在△OAB中,∠OAB=90°,
∵∠AOB=30°,
∴AB=
OB,∠COA=90°,
∴CE=AB,∠COA+∠OAB=180°,
∴CE∥AB,
∴四边形ABCE是平行四边形.
(2) 如图2,∵四边形ABCO折叠,点C与点A重合,折痕为EF,
∴△CEF≌△AEF,
∴EC=EA,
∵OB=4,
∴OC=BC=4,
在△OAB中,∠OAB=90°,
∵∠AOB=30°,
∴OA=2
,
在Rt△OAE中,由(1)知:∠EOA=90°,
设OE=x,
∵OE2+OA2=AE2,
∴x2+(2
)2=(4-x)2,
解得,x=
,
∴OE=
.
 ∴OC=OB,∠COB=60°.,
∴OC=OB,∠COB=60°.,∵点E是OC的中点,
∴EC=
| 1 |
| 2 |
| 1 |
| 2 |
在△OAB中,∠OAB=90°,
∵∠AOB=30°,
∴AB=
| 1 |
| 2 |
∴CE=AB,∠COA+∠OAB=180°,
∴CE∥AB,
∴四边形ABCE是平行四边形.
(2) 如图2,∵四边形ABCO折叠,点C与点A重合,折痕为EF,
∴△CEF≌△AEF,

∴EC=EA,
∵OB=4,
∴OC=BC=4,
在△OAB中,∠OAB=90°,
∵∠AOB=30°,
∴OA=2
| 3 |
在Rt△OAE中,由(1)知:∠EOA=90°,
设OE=x,
∵OE2+OA2=AE2,
∴x2+(2
| 3 |
解得,x=
| 1 |
| 2 |
∴OE=
| 1 |
| 2 |
看了 在△OAB中,∠OAB=90...的网友还看了以下:
选出每组单词中划括号部分读音不同的一项.1.A:t(o)day.B:t(o)morrow.C:st 2020-04-26 …
选出与所给单词划线部分读音相同的一项1、h(o)meA.c(o)meB.g(o)C.d(o)cto 2020-05-17 …
英语单词辨音找出画()部分读音与其余不同的单词()1.A .kn(ee) B.n(e)ck C.r 2020-05-17 …
选择元音字母在单词中发音不同的一项.1;A:h(a)nd;B:f(a)ce;C:(a)pple.2 2020-06-17 …
选择:诺a>b>o,c<d<o,则一定有()A,c分之a>d分之bB,c分之a<d分之b选择:诺a 2020-06-29 …
在三角形ABC中,sin(C一A)=1,sinB=三分之一.求sinA的值. 2020-07-13 …
绝对值代数式有理数abc在数轴上如图一一一一c一一一b一一0一一一a一一一(abc不是准确数/c/ 2020-07-31 …
已知a,b,c是三角形ABC的三边长,求证:a+b-c,a+c-b,b+c一a中至少有一个不大于a 2020-08-03 …
如图,在平面直角坐标系中,O为坐标原点,四边形OABC是长方形,点A、B、C、D的坐标分别为A(9, 2020-12-25 …
如图,在平面直角坐标系中,点A(-6,0)、点C(0,4),四边形OABC是矩形,以点O为圆心的⊙O 2020-12-25 …