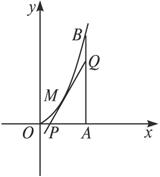
由y=0x=8y=x2围成曲边三角形在曲线弧OB上求一点M使得过M所作y=x2的切线PQ与OA、AB围成△PQA面积最大.

Question

由y=0 x=8 y=x ² 围成曲边三角形 在曲线弧OB上求一点M 使得过M所作y=x ² 的切线PQ与OA、AB围成△PQA面积最大.

Answer 1

解:由 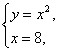得B(8 64).

    设M(x ₀ x ₀ ² ) k _PQ =2x ₀ (x ₀ ≠0).

    ∴PQ:y-x ₀ ² =2x ₀ (x-x ₀ )

    令y=0 得x=x ₀ - = .∴P( 0).

    令x=8 得y=x ₀ ² +16x ₀ -2x ₀ ² =16x ₀ -x ₀ ² .∴Q(8 16x ₀ -x ₀ ² ).

    S _{△ PQA} = (8- )·(16x ₀ -x ₀ ² )

    = x ₀ ³ -8x ₀ ² +64x ₀

    由S′=0得 x ₀ ² -16x ₀ +64=0

    ∴x ₀ = .

    ∴x ₀ =16(舍)或x ₀ = .∴M( ).