早教吧作业答案频道 -->数学-->
已知,如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.(1)求证:△ACE≌△BCD;(2)求证:2CD2=AD2+DB2.
题目详情
已知,如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
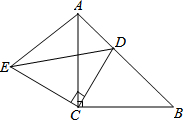
(1)求证:△ACE≌△BCD;
(2)求证:2CD2=AD2+DB2.

(1)求证:△ACE≌△BCD;
(2)求证:2CD2=AD2+DB2.
▼优质解答
答案和解析
证明:(1)∵△ABC和△ECD都是等腰直角三角形,
∴AC=BC,CD=CE,
∵∠ACB=∠DCE=90°,
∴∠ACE+∠ACD=∠BCD+∠ACD,
∴∠ACE=∠BCD,
在△ACE和△BCD中,
,
∴△AEC≌△BDC(SAS);
(2)∵△ACB是等腰直角三角形,
∴∠B=∠BAC=45度.
∵△ACE≌△BCD,
∴∠B=∠CAE=45°
∴∠DAE=∠CAE+∠BAC=45°+45°=90°,
∴AD2+AE2=DE2.
由(1)知AE=DB,
∴AD2+DB2=DE2,即2CD2=AD2+DB2.
∴AC=BC,CD=CE,
∵∠ACB=∠DCE=90°,
∴∠ACE+∠ACD=∠BCD+∠ACD,
∴∠ACE=∠BCD,
在△ACE和△BCD中,
|
∴△AEC≌△BDC(SAS);
(2)∵△ACB是等腰直角三角形,
∴∠B=∠BAC=45度.
∵△ACE≌△BCD,
∴∠B=∠CAE=45°
∴∠DAE=∠CAE+∠BAC=45°+45°=90°,
∴AD2+AE2=DE2.
由(1)知AE=DB,
∴AD2+DB2=DE2,即2CD2=AD2+DB2.
看了 已知,如图,△ACB和△EC...的网友还看了以下:
已知a分之一减a的绝对值等于1,则a分之一加a的绝对值为?已知a分之一减绝对值a等于1,则a分之一 2020-04-05 …
已知a等于2015,b等于2016,c等于2017,求a2+b2+c2-ab-ac-bc的值错了错 2020-05-20 …
已知A等于{a,b,c},B等于{-1,0,1},f是A到的映射,则满足f(a)+f(b)+f(c 2020-06-23 …
等级ABC票价(元/张)未知未知150北京2008年奥运会跳水决赛的门票价格如下表:小聪带了270 2020-06-27 …
在RT三角形ABC中,ab等于c,bc等于a,AC等于B,角c等于90度1已知a:b等于3:4,c 2020-07-22 …
在三角形ABC中,角A,B,C的对边分别是a,b,c,已知角A等于60度、sinB等于3sinC. 2020-07-22 …
已知a、b、c是ΔABC的三边,已知方程ax²+bx+c=0的相异两根之差的平方与cx²+bx+a 2020-08-02 …
1.已知a的平方加b的平方加c的平方减ab减bc减ca等于0.求证a等于b等于c2.已知3的n次方加 2020-11-01 …
已知f(x)=1/3x^3-1/2(a+1)在线等Y=X^2在(1,1)处的切线方程为!已知f(x) 2020-11-24 …
1.已知丨x丨小于等于1,求f(x)=x^2-2axa的最小值g(a)已知丨x丨小于等于1,求f(x 2020-12-01 …