早教吧作业答案频道 -->数学-->
在Rt△ABC中,∠ACB=90°,AC=BC,P是BC中垂线l上一动点,连接PA,交CB于点E,F是点E关于l的对称点.将PF延长交AB于点D,连接CD交PA于点G.(1)如图,若点P移动到BC下方时,求证:∠AEC=∠DFB,CD
题目详情
在Rt△ABC中,∠ACB=90°,AC=BC,P是BC中垂线l上一动点,连接PA,交CB于点E,F是点E关于l的对称点.将PF延长交AB于点D,连接CD交PA于点G.
(1)如图,若点P移动到BC下方时,求证:∠AEC=∠DFB,CD⊥AE;
(2)如图,若点P移动到BC的上方时,其他条件不变,请试写出线段AE、CD、DF的数量关系,并加以证明.
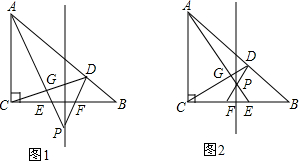
(1)如图,若点P移动到BC下方时,求证:∠AEC=∠DFB,CD⊥AE;
(2)如图,若点P移动到BC的上方时,其他条件不变,请试写出线段AE、CD、DF的数量关系,并加以证明.

▼优质解答
答案和解析
(2)证明:如图1,作∠ACB的角平分线交AP于H,
∵∠ACB=90°
∴∠BCH=∠ACH=45°
在Rt△ABC中
∵BC=AC
∴∠B=45°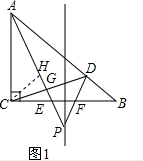
又∵P为BC的中垂线MN上一点,E,F关于l对称,
∴CE=BF,PE=PF,
∴∠PEF=∠PFE,
∴∠AEC=∠BFD,
在△CEH与△BFD中,
,
∴△CEH≌△BFD(ASA).
∴CH=BD,
在△ACH与△CBD中,
,
∴△ACH≌△CBD
∴∠BCD=∠CAH,
∵∠CAE+∠CEA=90°
∴∠GCE+∠CEG=90°
∴∠CGH=90°
∴CD⊥AE;
(2)AE=CD+DF,
证明:如图2,作∠ACB的角平分线交AP于H,
∵∠ACB=90°
∴∠BCH=∠ACH=45°
在Rt△ABC中
∵BC=AC
∴∠B=45°
又∵P为BC的中垂线MN上一点,E,F关于l对称,
∴CE=BF,PE=PF,
∴∠PEF=∠PFE,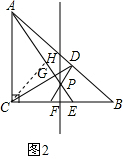
∴∠AEC=∠BFD,
在△CEH与△BFD中,
,
∴△CEH≌△BFD(ASA).
∴EH=FD,
在△ACH与△CBD中,
,
∴△ACH≌△CBD,
∴AH=CD,
∵AE=AH+EH,
∴AE=CD+DF.
∵∠ACB=90°
∴∠BCH=∠ACH=45°
在Rt△ABC中
∵BC=AC
∴∠B=45°

又∵P为BC的中垂线MN上一点,E,F关于l对称,
∴CE=BF,PE=PF,
∴∠PEF=∠PFE,
∴∠AEC=∠BFD,
在△CEH与△BFD中,
|
∴△CEH≌△BFD(ASA).
∴CH=BD,
在△ACH与△CBD中,
|
∴△ACH≌△CBD
∴∠BCD=∠CAH,
∵∠CAE+∠CEA=90°
∴∠GCE+∠CEG=90°
∴∠CGH=90°
∴CD⊥AE;
(2)AE=CD+DF,
证明:如图2,作∠ACB的角平分线交AP于H,
∵∠ACB=90°
∴∠BCH=∠ACH=45°
在Rt△ABC中
∵BC=AC
∴∠B=45°
又∵P为BC的中垂线MN上一点,E,F关于l对称,
∴CE=BF,PE=PF,
∴∠PEF=∠PFE,

∴∠AEC=∠BFD,
在△CEH与△BFD中,
|
∴△CEH≌△BFD(ASA).
∴EH=FD,
在△ACH与△CBD中,
|
∴△ACH≌△CBD,
∴AH=CD,
∵AE=AH+EH,
∴AE=CD+DF.
看了 在Rt△ABC中,∠ACB=...的网友还看了以下:
初二电学竞赛题将L3的E.F端与A.B分别接触,L1,L2,L3均发光,但亮度不足;将L3的E.F 2020-04-27 …
设函数f(x)=a^3+bx+c(a不等于0)为奇函数,其图像在(1,f(1))处的切线与直线x- 2020-05-13 …
已知,矩形ABCD中,AB=8cm,BC=16cm,AC的垂直平分线EF分别交AD,BC于点E,F 2020-05-16 …
初二几何问题,外加动点,急求!已知,矩形ABCD中,AB=4cm,bc=8cm,AC的垂直平分线E 2020-05-19 …
△ABC中,∠A为直角,在腰AB上任取一点P,连接CP,过A做AD垂直CP,交BC于D,垂足为M, 2020-05-22 …
物块静止在固定的斜面上,分别按图示的方向对物块施加大小相等的力F,A中F垂直于斜面向上.B中F垂直 2020-06-15 …
定义在[-1,1]上的奇函数f(x)满足f(1)=2,且当a,b∈[-1,1],a+b≠0时,有f 2020-07-20 …
菱形ABCD中,∠A=110°,AB的中垂线EP交AB于E,交CD于P,F是BC的中点,连接FP, 2020-08-01 …
数学平面几何问题两条平行直线l1和l2,在l1上取A,作AB垂直于l2交点为B,在l1上取C,连接 2020-08-02 …
在一个直角桌面上,桌角处有一个定滑轮,一根细绳连接两个物块(不计滑轮和细绳的质量).物块B为垂直吊在 2020-11-01 …