早教吧作业答案频道 -->数学-->
(1)如图(1),在四边形ABCD中,AB∥CD,如果延长DC到点E,使CE=AB,连接AE,那么有S四边形ABCD=S△ADE,作DE边中点P,连接AP,则AP所在直线为四边形ABCD的面积等分线,你能说明理由吗?(2)
题目详情
(1)如图(1),在四边形ABCD中,AB∥CD,如果延长DC到点E,使CE=AB,连接AE,那么有S四边形ABCD=S△ADE,作DE边中点P,连接AP,则AP所在直线为四边形ABCD的面积等分线,你能说明理由吗?
(2)如图(2),如果四边形ABCD中,AB与CD不平行,且S△ADC>S△ABC,过点A能否作出四边形ABCD的面积等分线?若能,请画出面积等分线,并简单说明作图过程.
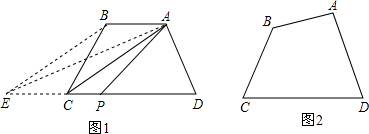 (1)如图(1),在四边形ABCD中,AB∥CD,如果延长DC到点E,使CE=AB,连接AE,那么有S四边形ABCD=S△ADE,作DE边中点P,连接AP,则AP所在直线为四边形ABCD的面积等分线,你能说明理由吗?
(1)如图(1),在四边形ABCD中,AB∥CD,如果延长DC到点E,使CE=AB,连接AE,那么有S四边形ABCD=S△ADE,作DE边中点P,连接AP,则AP所在直线为四边形ABCD的面积等分线,你能说明理由吗?
(2)如图(2),如果四边形ABCD中,AB与CD不平行,且S△ADC>S△ABC,过点A能否作出四边形ABCD的面积等分线?若能,请画出面积等分线,并简单说明作图过程.
 四边形ABCD=△ADE
四边形ABCD=△ADE
△ADC△ABC

(2)如图(2),如果四边形ABCD中,AB与CD不平行,且S△ADC>S△ABC,过点A能否作出四边形ABCD的面积等分线?若能,请画出面积等分线,并简单说明作图过程.
 (1)如图(1),在四边形ABCD中,AB∥CD,如果延长DC到点E,使CE=AB,连接AE,那么有S四边形ABCD=S△ADE,作DE边中点P,连接AP,则AP所在直线为四边形ABCD的面积等分线,你能说明理由吗?
(1)如图(1),在四边形ABCD中,AB∥CD,如果延长DC到点E,使CE=AB,连接AE,那么有S四边形ABCD=S△ADE,作DE边中点P,连接AP,则AP所在直线为四边形ABCD的面积等分线,你能说明理由吗?(2)如图(2),如果四边形ABCD中,AB与CD不平行,且S△ADC>S△ABC,过点A能否作出四边形ABCD的面积等分线?若能,请画出面积等分线,并简单说明作图过程.
 四边形ABCD=△ADE
四边形ABCD=△ADE△ADC△ABC

▼优质解答
答案和解析
(1)如图1中,∵AB∥EC,AB=EC,
∴四边形ABEC是平行四边形,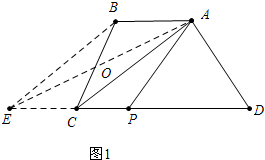
∴BE∥AC,
∴S△ACE△ACE=S△ACB△ACB,
∵S梯形ABCD梯形ABCD=S△ACB△ACB+S△ACD△ACD,S△AED△AED=S△ACE△ACE+S△ACD△ACD,
∴S△AED△AED=S梯形ABCD梯形ABCD,
∴S△AED△AED=S梯形ABCD梯形ABCD,
∵S梯形ABCD梯形ABCD=S△ACB△ACB+S△ACD△ACD,S△AED△AED=S△ACE△ACE+S△ACD△ACD,
∴S△AED△AED=S梯形ABCD梯形ABCD,
∵PE=PD,
∴S△APD△APD=
S△AED=
S梯形ABCD,
∴直线AP平分梯形ABCD的面积.
(2)如图2中,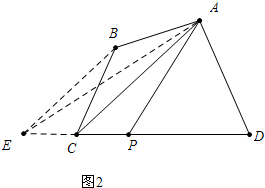 作BE∥AC交DC的延长线于E,连接AE,取DE中点,直线AP就是所求,理由如下:
作BE∥AC交DC的延长线于E,连接AE,取DE中点,直线AP就是所求,理由如下:
∵BE∥AC,
∴S△ACE=S△ACB,
∵S梯形ABCD=S△ACB+S△ACD,S△AED=S△ACE+S△ACD,
∴S△AED=S梯形ABCD,
∵PE=PD,
∴S△APD=
S△AED=
S梯形ABCD.
1 2 1 1 12 2 2S△AED△AED=
S梯形ABCD,
∴直线AP平分梯形ABCD的面积.
(2)如图2中, 作BE∥AC交DC的延长线于E,连接AE,取DE中点,直线AP就是所求,理由如下:
作BE∥AC交DC的延长线于E,连接AE,取DE中点,直线AP就是所求,理由如下:
∵BE∥AC,
∴S△ACE=S△ACB,
∵S梯形ABCD=S△ACB+S△ACD,S△AED=S△ACE+S△ACD,
∴S△AED=S梯形ABCD,
∵PE=PD,
∴S△APD=
S△AED=
S梯形ABCD.
1 2 1 1 12 2 2S梯形ABCD梯形ABCD,
∴直线AP平分梯形ABCD的面积.
(2)如图2中, 作BE∥AC交DC的延长线于E,连接AE,取DE中点,直线AP就是所求,理由如下:
作BE∥AC交DC的延长线于E,连接AE,取DE中点,直线AP就是所求,理由如下:
∵BE∥AC,
∴S△ACE△ACE=S△ACB△ACB,
∵S梯形ABCD梯形ABCD=S△ACB△ACB+S△ACD△ACD,S△AED△AED=S△ACE△ACE+S△ACD△ACD,
∴S△AED△AED=S梯形ABCD梯形ABCD,
∵PE=PD,
∴S△APD△APD=
S△AED=
S梯形ABCD.
1 2 1 1 12 2 2S△AED△AED=
S梯形ABCD.
1 2 1 1 12 2 2S梯形ABCD. 梯形ABCD.
∴四边形ABEC是平行四边形,

∴BE∥AC,
∴S△ACE△ACE=S△ACB△ACB,
∵S梯形ABCD梯形ABCD=S△ACB△ACB+S△ACD△ACD,S△AED△AED=S△ACE△ACE+S△ACD△ACD,
∴S△AED△AED=S梯形ABCD梯形ABCD,
∴S△AED△AED=S梯形ABCD梯形ABCD,
∵S梯形ABCD梯形ABCD=S△ACB△ACB+S△ACD△ACD,S△AED△AED=S△ACE△ACE+S△ACD△ACD,
∴S△AED△AED=S梯形ABCD梯形ABCD,
∵PE=PD,
∴S△APD△APD=
| 1 |
| 2 |
| 1 |
| 2 |
∴直线AP平分梯形ABCD的面积.
(2)如图2中,
 作BE∥AC交DC的延长线于E,连接AE,取DE中点,直线AP就是所求,理由如下:
作BE∥AC交DC的延长线于E,连接AE,取DE中点,直线AP就是所求,理由如下:∵BE∥AC,
∴S△ACE=S△ACB,
∵S梯形ABCD=S△ACB+S△ACD,S△AED=S△ACE+S△ACD,
∴S△AED=S梯形ABCD,
∵PE=PD,
∴S△APD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴直线AP平分梯形ABCD的面积.
(2)如图2中,
 作BE∥AC交DC的延长线于E,连接AE,取DE中点,直线AP就是所求,理由如下:
作BE∥AC交DC的延长线于E,连接AE,取DE中点,直线AP就是所求,理由如下:∵BE∥AC,
∴S△ACE=S△ACB,
∵S梯形ABCD=S△ACB+S△ACD,S△AED=S△ACE+S△ACD,
∴S△AED=S梯形ABCD,
∵PE=PD,
∴S△APD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴直线AP平分梯形ABCD的面积.
(2)如图2中,
 作BE∥AC交DC的延长线于E,连接AE,取DE中点,直线AP就是所求,理由如下:
作BE∥AC交DC的延长线于E,连接AE,取DE中点,直线AP就是所求,理由如下:∵BE∥AC,
∴S△ACE△ACE=S△ACB△ACB,
∵S梯形ABCD梯形ABCD=S△ACB△ACB+S△ACD△ACD,S△AED△AED=S△ACE△ACE+S△ACD△ACD,
∴S△AED△AED=S梯形ABCD梯形ABCD,
∵PE=PD,
∴S△APD△APD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
看了 (1)如图(1),在四边形A...的网友还看了以下:
1.设a.b.c分别是三角形ABC的三条边,且a/b=a+1/a+b+c,是判断∠A,∠B的关系. 2020-05-13 …
下列运算正确的是Aa的五次方+a的五次方=a的10次方Ba的六次方乘以a的四次方=a的二十四次方C 2020-05-14 …
由八个平行四边形组成的大平行四边形,一共可以数出几个平行四边形上边四个小平行四边形,下边四个小平行 2020-06-02 …
要一元一次方程解.设x分钟后壁虎和蝈蝈沿边长为6米的等边三角形房梁ABC的边按A→B→C→A的方向 2020-06-05 …
1.若平行四边形ABCD相似于平行四边形A'B'C'D',平行四边形ABCE的面积:平行四边形A' 2020-08-01 …
△ABC是⊙O的内接三角形,∠BAC=60°,D是的中点,AD=a,则四边形ABDC的面积为.△A 2020-08-03 …
若(2x-1)的四次方=a的四次方x的四次方+a3方x3方+a2方x2方+ax+a的零方.⑴求a的零 2020-11-07 …
壁虎和蝈蝈沿边长为6米的等边三角形房梁ABC的边按A→B→C→A的方向爬行,壁虎每分钟爬6.5米,蝈 2020-11-25 …
已知锐角三角形边a与角A求边b和边c可得b=a/A的正切值c=a/正弦值;已知锐角三角形边a与角B求 2020-12-25 …
(1)已知三角形ABC中2B=A+C,且边长b=3,c=2求边长a.(2)ABC面积为16(1)已知 2021-02-07 …