早教吧作业答案频道 -->数学-->
已知椭圆G:x26+y2b2=1(0<b<6)的两个焦点分别为F1和F2,短轴的两个端点分别为B1和B2,点P在椭圆G上,且满足|PB1|+|PB2|=|P
题目详情
已知椭圆G:
+
=1(0<b<
)的两个焦点分别为F1和F2,短轴的两个端点分别为B1和B2,点P在椭圆G上,且满足|PB1|+|PB2|=|PF1|+|PF2|.当b变化时,给出下列三个命题:
①点P的轨迹关于y轴对称;
②存在b使得椭圆G上满足条件的点P仅有两个;
③|OP|的最小值为2,
其中,所有正确命题的序号是___.
| x2 |
| 6 |
| y2 |
| b2 |
| | 6 |
①点P的轨迹关于y轴对称;
②存在b使得椭圆G上满足条件的点P仅有两个;
③|OP|的最小值为2,
其中,所有正确命题的序号是___.
▼优质解答
答案和解析
 椭圆G:
椭圆G:
+
=1(0<b<
)的两个焦点分别为
F1(
,0)和F2(-
,0),
短轴的两个端点分别为B1(0,-b)和B2(0,b),
设P(x,y),点P在椭圆G上,且满足|PB1|+|PB2|=|PF1|+|PF2|,
由椭圆定义可得,|PB1|+|PB2|=2a=2
>2b,
即有P在椭圆
+
=1上.
对于①,将x换为-x方程不变,则点P的轨迹关于y轴对称,
故①正确;
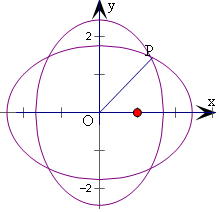
对于②,由图象可得轨迹关于x,y轴对称,且0<b<
,
则椭圆G上满足条件的点P有4个,
不存在b使得椭圆G上满足条件的点P仅有两个,故②不正确;
对于③,由图象可得,当P满足x2=y2,即有6-b2=b2,即b=
时,
|OP|取得最小值,可得x2=y2=2,即有|OP|的最小值为2,故③正确.
故答案为:①③.
 椭圆G:
椭圆G:| x2 |
| 6 |
| y2 |
| b2 |
| 6 |
F1(
| 6-b2 |
| 6-b2 |
短轴的两个端点分别为B1(0,-b)和B2(0,b),
设P(x,y),点P在椭圆G上,且满足|PB1|+|PB2|=|PF1|+|PF2|,
由椭圆定义可得,|PB1|+|PB2|=2a=2
| 6 |
即有P在椭圆
| y2 |
| 6 |
| x2 |
| 6-b2 |
对于①,将x换为-x方程不变,则点P的轨迹关于y轴对称,
故①正确;
对于②,由图象可得轨迹关于x,y轴对称,且0<b<
| 6 |
则椭圆G上满足条件的点P有4个,
不存在b使得椭圆G上满足条件的点P仅有两个,故②不正确;
对于③,由图象可得,当P满足x2=y2,即有6-b2=b2,即b=
| 3 |
|OP|取得最小值,可得x2=y2=2,即有|OP|的最小值为2,故③正确.
故答案为:①③.
看了 已知椭圆G:x26+y2b2...的网友还看了以下:
已知椭圆x2a2+y2b2=1(a>b>0)的左焦点F1和右焦点F2,上顶点为A,AF2的中垂线交 2020-06-16 …
已知抛物线C:y2=2px(p>0)的焦点F和椭圆的右焦点重合,直线过点F交抛物线于A、B两点.( 2020-06-21 …
椭圆焦点的物理意义?椭圆焦点在学习数学时已经清楚了,既然叫焦点就和物理李学的焦点有关,到底是什么关 2020-06-30 …
已知椭圆的中心在原点他在x轴上的一个焦点与短轴的两个端点B1B2已知椭圆的中心在坐标原点,它在X轴 2020-07-09 …
如图,F1和F2分别是双曲线x^2/a^2-y^2/b^2=1(a>0,b>0)的两个焦点,A和B 2020-07-26 …
圆锥曲线2双曲线的焦点F1和F2在轴上,点P在双曲线上,如果线段PF1的中点在y轴上,线段PF2的 2020-07-30 …
两个面只有一个焦点公理3说两面相交会有一个公共线,如果两面相交只有一个焦点,别说不可能,一个面的角 2020-07-30 …
已知一个椭圆的左焦点及相应的准线与抛物线y^2=8x的焦点F和准线l分别重合(1)求椭圆的短轴的端 2020-07-31 …
物体AB被置于一薄透镜的焦点F和光心O之间,并垂直于透镜的主轴.透镜的大小、焦点的位置、物体AB的 2020-08-01 …
设椭圆x平方/25+y平方/9=1上一点p的横坐标是2求点p到椭圆左焦点PF1和右焦点的距离PF2 2020-11-07 …