早教吧作业答案频道 -->数学-->
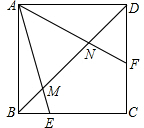
正方形ABCD中,∠EAF=45°,连接对角线BD交AE于M,交AF于N,求证:以DN、BM、MN为三边的三角形为直角三角形.
题目详情
正方形ABCD中,∠EAF=45°,连接对角线BD交AE于M,交AF于N,求证:以DN、BM、MN为三边的三角形为直角三角形.

▼优质解答
答案和解析
证明:延长CB到G,使BG=DF,连接AG,在AG截取AH=AN,连接MH、BH,如图所示: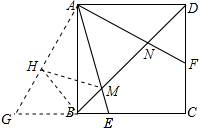
∵四边形ABCD为正方形,
∴AB=BC=CD=AD,∠BDC=∠ABD=45°,∠BAD=∠ADF=∠ABE=∠ABG=90°,
在△ABG和△ADF中,
,
∴△ABG≌△ADF(SAS),
∴∠BAG=∠DAF,∠AFD=∠G,AF=AG,
∴∠GAE=∠BAG+∠BAE=∠DAF+∠BAE=∠BAD-∠EAF=90°-45°=45°=∠EAF,
在△AMN和△AMH中,
,
∴△AMN≌△AMH(SAS),
∴MN=MH,
∵AF=AG,AN=AH,
∴FN=AF-AN=AG-AH=GH,
在△DFN和△BGH中,
,
∴△DFN≌△BGH(SAS),
∴∠GBH=∠NDF=45°,DN=BH,
∴∠MBH=∠ABH+∠ABD=∠ABG-∠GBH+∠ABD=90°-45°+45°=90°,
∴BM2+DN2=BM2+BH2=MH2=MN2,
∴DN、BM、MN为三边的三角形为直角三角形.

∵四边形ABCD为正方形,
∴AB=BC=CD=AD,∠BDC=∠ABD=45°,∠BAD=∠ADF=∠ABE=∠ABG=90°,
在△ABG和△ADF中,
|
∴△ABG≌△ADF(SAS),
∴∠BAG=∠DAF,∠AFD=∠G,AF=AG,
∴∠GAE=∠BAG+∠BAE=∠DAF+∠BAE=∠BAD-∠EAF=90°-45°=45°=∠EAF,
在△AMN和△AMH中,
|
∴△AMN≌△AMH(SAS),
∴MN=MH,
∵AF=AG,AN=AH,
∴FN=AF-AN=AG-AH=GH,
在△DFN和△BGH中,
|
∴△DFN≌△BGH(SAS),
∴∠GBH=∠NDF=45°,DN=BH,
∴∠MBH=∠ABH+∠ABD=∠ABG-∠GBH+∠ABD=90°-45°+45°=90°,
∴BM2+DN2=BM2+BH2=MH2=MN2,
∴DN、BM、MN为三边的三角形为直角三角形.
看了 正方形ABCD中,∠EAF=...的网友还看了以下:
在△ABC钟,以BC为直径的圆O交AB于D点,交AC于E点,AD=3,SADE=S四边形BCDE, 2020-06-02 …
如图,平面直角坐标系中,直线AB:y=−13x+b交y轴于点A(0,1),交x轴于点B.直线x=1 2020-06-08 …
如图平面直角坐标系中,抛物线y=-x2+x+2交x轴于A、B两点,交y轴于点C.(1)求证:△AB 2020-06-14 …
在平面直角坐标系中,直线L1:y=2x+b交x轴正半轴于点A,点B(4,0)在点A的右边,现过点B 2020-06-14 …
如图,在平面直角坐标系中,直线AB:y=kx+1(k≠0)交y轴于点A,交x轴于点B(3,0),平 2020-06-23 …
E为三角形ABC中AB边的中点,D为三角形ABC外一点,E为三角形ABC中AB边的重点,D为三角形 2020-07-22 …
如果两条平行线被第三条直线所截,那么一组同位角的平分线()A.互相平行B.互相垂直C.交角是锐角D 2020-07-23 …
在三角形ABC中,角B=22.5度,AB的垂直平分线交AB于点Q,交BC于点P,PE垂直AC,垂足 2020-08-03 …
数学题在线解答已知集合A={三角形},B={等腰三角形},C={等边三角形},D={直角三角形},那 2020-11-27 …
请先画一个直角三角形ABC,使∠C=90°,再画两锐角∠A,∠B的角平分线AO、BO交于点O.(1) 2020-12-09 …