早教吧作业答案频道 -->数学-->
如图,在△ABC中∠ABC=45°,CD⊥BA,BE⊥AC,F为BC中点,∠ABE=∠CBE(1)线段BH与线段AC相等吗?若相等给予证明,若不相等,请说明理由.(2)若AC=12,BC=10,求BG的长.
题目详情
如图,在△ABC中∠ABC=45°,CD⊥BA,BE⊥AC,F为BC中点,∠ABE=∠CBE
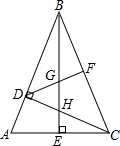
(1)线段BH与线段AC相等吗?若相等给予证明,若不相等,请说明理由.
(2)若AC=12,BC=10,求BG的长.

(1)线段BH与线段AC相等吗?若相等给予证明,若不相等,请说明理由.
(2)若AC=12,BC=10,求BG的长.
▼优质解答
答案和解析
(1)线段BH与线段AC相等.
证明:∵CD⊥AB,BE⊥AC,
∴∠BDH=∠BEC=∠CDA=90°,
∵∠ABC=45°,
∴∠BCD=180°-90°-45°=45°=∠ABC,
∴DB=DC,
∵∠BDH=∠BEC=∠CDA=90°,
∴∠A+∠ACD=90°,∠A+∠HBD=90°,
∴∠HBD=∠ACD,
∵在△DBH和△DCA中,
,
∴△DBH≌△DCA(ASA),
∴BH=AC;
(2)如图,连接CG,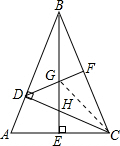
由(1)知,DB=CD,
∵F为BC的中点,
∴DF垂直平分BC,
∴BG=CG,
∵∠ABE=∠CBE,BE⊥AC,
∴△ABE≌△CBE,
∴EC=EA=6,
∵Rt△BCE中,BC=10,CE=6,
∴BE=8,
设BG=CG=x,则GE=8-x,
∴Rt△CEH中,62+(8-x)2=x2,
∴x=
,
∴BG=
.
证明:∵CD⊥AB,BE⊥AC,
∴∠BDH=∠BEC=∠CDA=90°,
∵∠ABC=45°,
∴∠BCD=180°-90°-45°=45°=∠ABC,
∴DB=DC,
∵∠BDH=∠BEC=∠CDA=90°,
∴∠A+∠ACD=90°,∠A+∠HBD=90°,
∴∠HBD=∠ACD,
∵在△DBH和△DCA中,
|
∴△DBH≌△DCA(ASA),
∴BH=AC;
(2)如图,连接CG,

由(1)知,DB=CD,
∵F为BC的中点,
∴DF垂直平分BC,
∴BG=CG,
∵∠ABE=∠CBE,BE⊥AC,
∴△ABE≌△CBE,
∴EC=EA=6,
∵Rt△BCE中,BC=10,CE=6,
∴BE=8,
设BG=CG=x,则GE=8-x,
∴Rt△CEH中,62+(8-x)2=x2,
∴x=
| 25 |
| 4 |
∴BG=
| 25 |
| 4 |
看了 如图,在△ABC中∠ABC=...的网友还看了以下:
是否存在正整数a,b,使其满足根号a+根号b=根号275?若存在,请求出是否存在正整数a,b,使其 2020-05-15 …
是否存在正整数m,使(a+b)的4m-1次方能被(a+b)2m+7次方整除?若存在,求m的值,若不 2020-05-15 …
△ABC的三边长分别为:AB=2a²-a-7,BC=10-a²,AC=a 超级急,①求△ABC的周 2020-05-16 …
下面的叙述中正确的是______。A.在请求页式存储管理中,当进程对页面淘汰时,进行地址转换操作。B 2020-05-24 …
我国专利申请的原则之一是“(10)”。A.申请在先B.申请在先与使用在先相结合C.使用在先D.申请在 2020-05-26 …
我国专利申请的原则之一是(7)。A.申请在先B.申请在先与使用在先相结合C.使用在先D.申请在先、使 2020-05-26 …
我国专利申请的原则之一是“(21)”。A.申请在先B.申请在先与使用在先相结合C.使用在先D.申请在 2020-05-26 …
我国专利申请的原则之一是(10)。A.申请在先B.申请在先与使用在先相结合C.使用在先D.申请在先、 2020-05-26 …
高难度数学函数题f(x)=xsin(a/x)函数f(x)=xsin(a/x),a不等于0.问a是否 2020-06-13 …
1.已知点A(2,3),B(4,5)在x轴上是否存在点P使|PA-PB|的值最小,若存在,请求出点 2020-07-26 …