早教吧作业答案频道 -->数学-->
如图,在菱形ABCD中,∠B=60°,若AB=2,点E是BC边上一动点,∠EAF=60°,AF交CD于点F(1)探究线段AE、AF的数量关系,并写出解答过程;(2)当点E运动到什么位置时,△AEF的面积最小,最小面
题目详情
如图,在菱形ABCD中,∠B=60°,若AB=2,点E是BC边上一动点,∠EAF=60°,AF交CD于点F
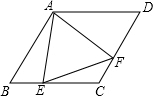
(1)探究线段AE、AF的数量关系,并写出解答过程;
(2)当点E运动到什么位置时,△AEF的面积最小,最小面积是多少?

(1)探究线段AE、AF的数量关系,并写出解答过程;
(2)当点E运动到什么位置时,△AEF的面积最小,最小面积是多少?
▼优质解答
答案和解析
(1)AE=AF,理由如下:
连接AC.如图所示:
∵四边形ABCD是菱形,
∴AB=BC,∵∠B=60°,
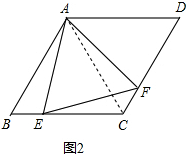 ∴△ABC是等边三角形,
∴△ABC是等边三角形,
∴AB=AC,∠ACB=60°.
∴∠B=∠ACF=60°.
∵AD∥BC,
∴∠AEB=∠EAD=∠EAF+∠FAD=60°+∠FAD,∠AFC=∠D+∠FAD=60°+∠FAD.
∴∠AEB=∠AFC.
在△ABE和△ACF中,
,
∴△ABE≌△ACF(AAS).
∴AE=AF.
(3)由垂线段最短可知:当AE⊥BC时,AE有最小值.
∵AE=AF.∠EAF=60°,
∴△AEF是等边三角形.
∵AE⊥BC,∠B=60°,
∴AE=AB•sin60°=2×
=
,
∴EF=
,此时△AEF的面积=
×
×
×
=
;
当AE⊥BC时,△AEF的面积最小,最小面积是
连接AC.如图所示:
∵四边形ABCD是菱形,
∴AB=BC,∵∠B=60°,
 ∴△ABC是等边三角形,
∴△ABC是等边三角形,∴AB=AC,∠ACB=60°.
∴∠B=∠ACF=60°.
∵AD∥BC,
∴∠AEB=∠EAD=∠EAF+∠FAD=60°+∠FAD,∠AFC=∠D+∠FAD=60°+∠FAD.
∴∠AEB=∠AFC.
在△ABE和△ACF中,
|
∴△ABE≌△ACF(AAS).
∴AE=AF.
(3)由垂线段最短可知:当AE⊥BC时,AE有最小值.
∵AE=AF.∠EAF=60°,
∴△AEF是等边三角形.
∵AE⊥BC,∠B=60°,
∴AE=AB•sin60°=2×
| ||
| 2 |
| 3 |
∴EF=
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
3
| ||
| 4 |
当AE⊥BC时,△AEF的面积最小,最小面积是
3
|
看了 如图,在菱形ABCD中,∠B...的网友还看了以下:
下列装置或操作合理的是()A.装置①可用于实验室制取少量氯气B.装置②可用于实验室制取少量乙烯C. 2020-04-08 …
下列有关实验装置及用途叙述正确的是()A.装置用于检验消去产物B.装置检验酸性:盐酸>碳酸>苯酚C 2020-04-08 …
下列有关实验装置及用途叙述完全正确的是A.a装置检验消去产物,中间应加水洗装置B.b装置检验酸性: 2020-04-08 …
下列实验装置图能完成相应实验的是()A.装置①可用于实验室制取乙酸乙酯B.装置②可用于分离苯和甲苯 2020-04-08 …
关于如图各装置的叙述正确的是()A.装置①可用于实验室制备NO气体B.装置②可用于模拟海水蒸馏C. 2020-04-12 …
今年的春分日是3月21日,当日地球处于图中:()A.a位置B.b位置C.c位置D.d位置 2020-05-04 …
下列实验装置进行的相应实验,能达到实验目的的是A.装置甲可用于检验有乙烯生成B.装置乙可用于收集和 2020-05-14 …
已知高炉炼铁的化学方程式为Fe2O3+3CO=2Fe+3CO2注:高温条件下列对该反应的叙述不正确 2020-05-14 …
下列对各实验装置用途的叙述,不正确的是()A.装置①可用于分离C2H5OH和CH3COOCH2CH 2020-05-17 …
关于下列各实验装置的叙述中,不正确的是()A.装置①可用于分离C2H5OH和H2O的混合物B.装置 2020-07-03 …
 扫描下载二维码
扫描下载二维码