已知，如图，在平面直角坐标系xOy中，二次函数y=ax2-73x+c的图象经过点、A（0，8）、B（6，2）、C（9，m），延长AC交x轴于点D．（1）求这个二次函数的解析式及的m值；（2）求∠ADO的余切值；

Question

已知，如图，在平面直角坐标系xOy中，二次函数y=ax²-(7)/(3)x+c的图象经过点、A（0，8）、B（6，2）、C（9，m），延长AC交x轴于点D．

（1）求这个二次函数的解析式及的m值；
（2）求∠ADO的余切值；
（3）过点B的直线分别与y轴的正半轴、x轴、线段AD交于点P（点A的上方）、M、Q，使以点P、A、Q为顶点的三角形与△MDQ相似，求此时点P的坐标．

Answer 1

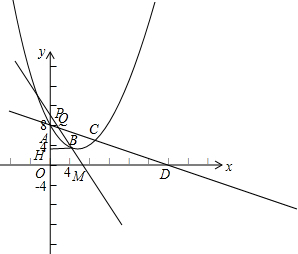（1）把A（0，8）、B（6，2）代入y=ax²-(7)/(3)x+c，得

8=c

2=a×62-(7)/(3)×6+c

，
解得

a=(2)/(9)

c=8

，
故该二次函数解析式为：y=(2)/(9)x²-(7)/(3)x+8．
把C（9，m），代入y=(2)/(9)x²-(7)/(3)x+8得到：m=y=(2)/(9)×9²-(7)/(3)×9+8=5，即m=5．
综上所述，该二次函数解析式为y=(2)/(9)x²-(7)/(3)x+8，m的值是5；

（2）由（1）知，点C的坐标为：（9，5），
又由点A的坐标为（0，8），
所以直线AC的解析式为：y=-(1)/(3)x+8，
令y=0，则0=-(1)/(3)x+8，
解得x=24，
即OD=24，
所以cot∠ADO=(OD)/(OA)=(24)/(8)=3，即cot∠ADO=3；

（3）在△APQ与△MDQ中，∠AQP=∠MQD．
要使△APQ与△MDQ相似，则∠APQ=∠MDQ或∠APQ=∠DMQ（根据题意，这种情况不可能），
∴cot∠APQ=cot∠MDQ=3．
作BH⊥y轴于点H，
在直角△PBH中，cot∠P=(PH)/(BH)=3，
∴PH=18，OP=20，
∴点P的坐标是（0，20）．