早教吧作业答案频道 -->数学-->
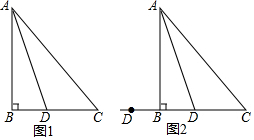
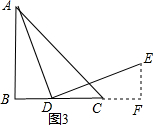
在△ABC中,AB=BC,∠B=90°,点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.(1)如果点D在线段BC上运动,如图1:①依题
题目详情
在△ABC中,AB=BC,∠B=90°,点D为直线BC上的一个动点(不与B、C重合),连结AD,将线段AD绕点D按顺时针方向旋转90°,使点A旋转到点E,连结EC.
(1)如果点D在线段BC上运动,如图1:
①依题意补全图1;
②求证:∠BAD=∠EDC;
③通过观察、实验,小明得出结论:在点D运动的过程中,总有∠DCE=135°,.
小明与同学讨论后,形成了证明这个结论的几种想法:
想法一:在AB上取一点F,使得BF=BD,要证∠DCE=135°,只需证△ADF≌△DEC.
想法二:以点D为圆心,DC为半径画弧交AC于点F,要证∠DCE=135°,只需证△AFD≌△DCE.
想法三:过点E作BC所在直线的垂直线段EF,要证∠DCE=135°,只需证EF=CF.
…
请你参考上面的想法,证明∠DCE=135°
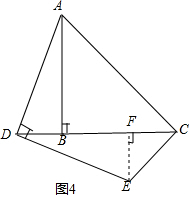
(2)如果点D在线段CB的延长线上运动,利用图2画图分析,∠DCE的度数还是确定的值吗?如果是,直接写出∠DCE的度数;如果不是,说明理由.

(1)如果点D在线段BC上运动,如图1:
①依题意补全图1;
②求证:∠BAD=∠EDC;
③通过观察、实验,小明得出结论:在点D运动的过程中,总有∠DCE=135°,.
小明与同学讨论后,形成了证明这个结论的几种想法:
想法一:在AB上取一点F,使得BF=BD,要证∠DCE=135°,只需证△ADF≌△DEC.
想法二:以点D为圆心,DC为半径画弧交AC于点F,要证∠DCE=135°,只需证△AFD≌△DCE.
想法三:过点E作BC所在直线的垂直线段EF,要证∠DCE=135°,只需证EF=CF.
…
请你参考上面的想法,证明∠DCE=135°
(2)如果点D在线段CB的延长线上运动,利用图2画图分析,∠DCE的度数还是确定的值吗?如果是,直接写出∠DCE的度数;如果不是,说明理由.
▼优质解答
答案和解析
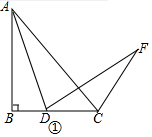 (1)①如图①所示;
(1)①如图①所示;
②证明:∵∠B=90°,
∴∠BAD+∠BDA=90°,
∵∠ADE=90°,点D在线段BC上,
∴∠BAD+∠EDC=90°,
∴∠BAD=∠EDC;
②证法1:如图1,在AB上取点F,使得BF=BD,连接DF,
∵BF=BD,∠B=90°,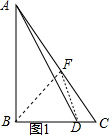
∴∠BFD=45°,
∴∠AFD=135°,
∵BA=BC,
∴AF=CD,
在△ADF和△DEC中,
,
∴△ADF≌△DEC,
∴∠DCE=∠AFD=135°;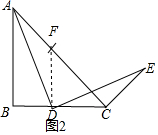
证法2:以D为圆心,DC为半径作弧交AC于点F,连接DF,
∴DC=DF,∠DFC=∠DCF,
∵∠B=90°,AB=BC,
∴∠ACB=45°,∠DFC=45°,
∴∠DFC=90°,∠AFD=135°,
∵∠ADE=∠FDC=90°,
∴∠ADF=∠EDC,
在△ADF≌△CDE中,
,
∴△ADF≌△CDE,
∴∠AFD=∠DCE=135°;
证法3:过点E作EF⊥BC交BC的延长线于点F,
∴∠EFD=90°,
∵∠B=90°,
∴∠EFD=∠B,
在△ABD和△DFE中,
,
∴△ABD≌△DFE,
∴AB=DF,BD=EF,
∵AB=BC,
∴BC=DF,BC-DC=DF-DC,
即BD=CF,
∴EF=CF,
∵∠EFC=90°,
∴∠ECF=45°,∠DCE=135°;
(2) ∠DCE=45°,
理由:过E作EF⊥DC于F,
∵∠ABD=90°,
∴∠EDF=∠DAB=90°-∠ADB,
在△ABD和△DFE中,
,
∴△ABD≌△DFE,
∴DB=EF,AB=DF=BC,
∴BC-BF=DF-BF,
即FC=DB,
∴FC=EF,
∴∠DCE=45°.
 (1)①如图①所示;
(1)①如图①所示;②证明:∵∠B=90°,
∴∠BAD+∠BDA=90°,
∵∠ADE=90°,点D在线段BC上,
∴∠BAD+∠EDC=90°,
∴∠BAD=∠EDC;
②证法1:如图1,在AB上取点F,使得BF=BD,连接DF,
∵BF=BD,∠B=90°,

∴∠BFD=45°,
∴∠AFD=135°,
∵BA=BC,
∴AF=CD,
在△ADF和△DEC中,
|
∴△ADF≌△DEC,
∴∠DCE=∠AFD=135°;

证法2:以D为圆心,DC为半径作弧交AC于点F,连接DF,
∴DC=DF,∠DFC=∠DCF,
∵∠B=90°,AB=BC,
∴∠ACB=45°,∠DFC=45°,
∴∠DFC=90°,∠AFD=135°,
∵∠ADE=∠FDC=90°,
∴∠ADF=∠EDC,
在△ADF≌△CDE中,
|

∴△ADF≌△CDE,
∴∠AFD=∠DCE=135°;
证法3:过点E作EF⊥BC交BC的延长线于点F,
∴∠EFD=90°,
∵∠B=90°,
∴∠EFD=∠B,
在△ABD和△DFE中,
|

∴△ABD≌△DFE,
∴AB=DF,BD=EF,
∵AB=BC,
∴BC=DF,BC-DC=DF-DC,
即BD=CF,
∴EF=CF,
∵∠EFC=90°,
∴∠ECF=45°,∠DCE=135°;
(2) ∠DCE=45°,
理由:过E作EF⊥DC于F,
∵∠ABD=90°,
∴∠EDF=∠DAB=90°-∠ADB,
在△ABD和△DFE中,
|
∴△ABD≌△DFE,
∴DB=EF,AB=DF=BC,
∴BC-BF=DF-BF,
即FC=DB,
∴FC=EF,
∴∠DCE=45°.
看了 在△ABC中,AB=BC,∠...的网友还看了以下:
如图所示,空中有三个点电荷A,B,C,质量均为m;A和B所带电荷量为+Q,C所带电荷量为-Q,AB 2020-05-13 …
如何绕10寸单线电机如题10寸30磁钢多线电机拆了准备绕单线不知怎么绕线圈背面是如何跳绕的?是用2 2020-05-16 …
靠在一起的M,N两转盘靠摩擦转动,两盘均绕过圆心的竖直轴转动,M盘的半径为r,N盘的半径R=2r, 2020-06-20 …
ao=bo=1/2,oa⊥ob.如图,点c是射线ab上一动点,连接oc,将oc绕c顺时针旋转90° 2020-06-20 …
第二性曲线积分一题.已知曲线积分∮cxdy-ydx/(f(x)+y2)=A(常数),其中f(x)为 2020-07-12 …
有一台星形连接的三相交流发电机,额定相电压为660V若测得其线电压UAB=660V,UBC=660 2020-07-20 …
如图所示,U形线圈上绕有两个线圈,为了使它能作为电磁铁正常使用,这两组线圈的正确连法是[]A.b、 2020-08-01 …
如果两个图形可通过旋转而相互得到,则下列说法中错误的是()A.对应点连线的中垂线必经过旋转中心B. 2020-08-01 …
如图所示,线圈I与电源、开关、滑动变阻器相连,线圈Ⅱ与电流计G相连,线圈I与线圈Ⅱ绕在同一个铁芯上, 2020-12-20 …
在平面直角坐标系中,点A坐标为(-2,4),与原点的连线OA绕原点顺时针转90°,得到线段OB,连接 2021-02-04 …