早教吧作业答案频道 -->数学-->
已知等腰Rt△ABC与等腰Rt△CDE,∠ACB=∠DCE=90°,把Rt△ABC绕点C旋转.(1)如图1,当点A旋转到ED的延长线时,若BC=1322,BE=5,求CD的长;(2)当Rt△ABC旋转到如图2所示的位置时,过点C作BD的垂
题目详情
已知等腰Rt△ABC与等腰Rt△CDE,∠ACB=∠DCE=90°,把Rt△ABC绕点C旋转.
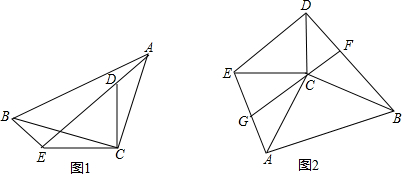
(1)如图1,当点A旋转到ED的延长线时,若BC=
,BE=5,求CD的长;
(2)当Rt△ABC旋转到如图2所示的位置时,过点C作BD的垂线交BD于点F,交AE于点G,求证:BD=2CG.

(1)如图1,当点A旋转到ED的延长线时,若BC=
13
| ||
| 2 |
(2)当Rt△ABC旋转到如图2所示的位置时,过点C作BD的垂线交BD于点F,交AE于点G,求证:BD=2CG.
▼优质解答
答案和解析
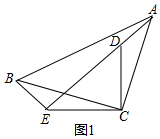 (1)如图1,∵△ADC是由△BEC绕点C旋转得到的,
(1)如图1,∵△ADC是由△BEC绕点C旋转得到的,
∴AD=BE=5,∠ADC=∠BEC,
∵在等腰Rt△ABC与等腰Rt△CDE中,BC=AC=
,∠EDC=∠DEC=45°,
∴AB=13,∠ADC=∠BEC=135°,
∴∠AEB=90°,
∴AE=
=12,
∴DE=7,
∴等腰Rt△CDE中,CD=
DE=
;
(2)如图2,过点A作AH∥CE,交CG的延长线于H,连接HE,则∠CAH+∠ACE=180°,
∵∠ACB=∠DCE=90°,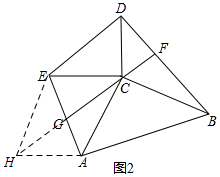
∴∠BCD+∠ACE=180°,
∴∠CAE=∠BCD,
∵CF⊥BD,∠ACB=90°,
∴∠CBF+∠BCF=∠ACG+∠BCF=90°,
∴∠CBF=∠ACG,
在△BCD和△CAH中,
,
∴△BCD≌△CAH(ASA),
∴AH=CD=CE,BD=CH,
又∵AH∥CE,
∴四边形ACEH是平行四边形,
∴CH=2CG,
∴BD=2CG.
 (1)如图1,∵△ADC是由△BEC绕点C旋转得到的,
(1)如图1,∵△ADC是由△BEC绕点C旋转得到的,∴AD=BE=5,∠ADC=∠BEC,
∵在等腰Rt△ABC与等腰Rt△CDE中,BC=AC=
13
| ||
| 2 |
∴AB=13,∠ADC=∠BEC=135°,
∴∠AEB=90°,
∴AE=
| AB2-BE2 |
∴DE=7,
∴等腰Rt△CDE中,CD=
| ||
| 2 |
7
| ||
| 2 |
(2)如图2,过点A作AH∥CE,交CG的延长线于H,连接HE,则∠CAH+∠ACE=180°,
∵∠ACB=∠DCE=90°,

∴∠BCD+∠ACE=180°,
∴∠CAE=∠BCD,
∵CF⊥BD,∠ACB=90°,
∴∠CBF+∠BCF=∠ACG+∠BCF=90°,
∴∠CBF=∠ACG,
在△BCD和△CAH中,
|
∴△BCD≌△CAH(ASA),
∴AH=CD=CE,BD=CH,
又∵AH∥CE,
∴四边形ACEH是平行四边形,
∴CH=2CG,
∴BD=2CG.
看了 已知等腰Rt△ABC与等腰R...的网友还看了以下:
已知A、B、C是三根相同材料的导线,A和B的长度相同,A比B细;B和C的粗细相同,B比C长.那么这 2020-04-13 …
如图,已知在△ABC中,∠ACB=90°,AC=BC,直线MN过C点,AD⊥MN于D点,BE⊥MN 2020-05-16 …
1.当光线射到x轴的点C后进行反射,如果反射的路径经过点A(0,1)和点B(3,4),则入射光线所 2020-05-23 …
已知,如图b,c为定长线段ad上的两个动点(ad长度保持一定,b在c点左侧)(1)当b,c运动到某 2020-06-05 …
如图,已知定长线短AD=m,B、C为线段AD上的两个动点,B在C的左侧(1)当B、C运动到某一位置 2020-06-05 …
如图,B,C为定长线段AD上的两个动点(AD长度保持一定,B点在C点的左侧).1,当B,C运动到某 2020-06-05 …
在正方形ABCD中,BD是一条对角线,点P在射线CD上(与点C、D不重合),连接AP,平移△ADP 2020-06-12 …
如图所示,长为L的悬线固定在O点,在O点正下方L2处有一钉子C,把悬线另一端的小球m拉到跟悬点在同 2020-06-26 …
(2014•广元二模)等量异种点电荷+Q和-Q固定,在它们的连线和中垂线上有a、b、c三点,如图所示 2020-11-12 …
如果图中箭头①②③④表示我国的远洋航线,下列说法正确的是()A.①表示到达美国东海岸的航线B.②表示 2020-12-05 …