早教吧作业答案频道 -->数学-->
如图,在边长为6的正方形ABCD中,点E为边AD上的一个动点(与点A、D不重合),∠EBM=45°,BE交对角线AC于点F,BM交于AC于点G,交CD于点M.(1)求DE:CG的值;(2)设AE=x,S△BEG=y.①求y关于x
题目详情
如图,在边长为6的正方形ABCD中,点E为边AD上的一个动点(与点A、D不重合),∠EBM=45°,BE交对角线AC于点F,BM交于AC于点G,交CD于点M.
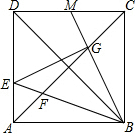
(1)求DE:CG的值;
(2)设AE=x,S△BEG=y.
①求y关于x的函数表达式及x的取值范围.
②当图中点E、M关于对角线BD成轴对称时,求y的值.

(1)求DE:CG的值;
(2)设AE=x,S△BEG=y.
①求y关于x的函数表达式及x的取值范围.
②当图中点E、M关于对角线BD成轴对称时,求y的值.
▼优质解答
答案和解析
 (1)∵四边形ABCD是正方形,
(1)∵四边形ABCD是正方形,
∴∠BDE=∠BCG=∠CBD=45°,BD=
BC,
∵∠EBM=45°,
∴∠DBE=∠CBG,
∴△BDE∽△BCG,
∴DE:CG=BD:BC=
:1;
(2)①∵四边形ABCD是正方形,且△BDE∽△BCG,
∴BE:BG=BD:BC=BD:AB=
:1,
∴△BEG∽△BAD,
∴△BEG为等腰直角三角形,
∴y=S△BEG=
NE2=
x2+9(0<x<6);
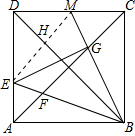
②若E、M关于对角线BD成轴对称,连接EM,交AC于点H,
∴BD垂直平分EM,BE平分∠ABD,
∴AE=HE=DH,DE=
HE,
∴6-x=
x,即x=6
-6,
则y=
×(6
-6)2+9=36-18
.
 (1)∵四边形ABCD是正方形,
(1)∵四边形ABCD是正方形,∴∠BDE=∠BCG=∠CBD=45°,BD=
| 2 |
∵∠EBM=45°,
∴∠DBE=∠CBG,
∴△BDE∽△BCG,
∴DE:CG=BD:BC=
| 2 |
(2)①∵四边形ABCD是正方形,且△BDE∽△BCG,
∴BE:BG=BD:BC=BD:AB=
| 2 |
∴△BEG∽△BAD,
∴△BEG为等腰直角三角形,
∴y=S△BEG=
| 1 |
| 4 |
| 1 |
| 4 |
②若E、M关于对角线BD成轴对称,连接EM,交AC于点H,
∴BD垂直平分EM,BE平分∠ABD,
∴AE=HE=DH,DE=
| 2 |
∴6-x=
| 2 |
| 2 |
则y=
| 1 |
| 4 |
| 2 |
| 2 |
看了 如图,在边长为6的正方形AB...的网友还看了以下:
抛物线y=ax²+bx+3与y轴交于点C,与x轴交于A、B两点,tan∠OCA=⅓,SΔABC=6 2020-05-16 …
选用所给的句子完成下列对话,将句子抄写在相应的横线上.E:Hobo,todayisHallowee 2020-05-16 …
一次函数问题(写出解题过程)直线y+kx=6与x轴、y轴分别交与点E、F,点E的坐标为(-8,0) 2020-05-20 …
直线Y=kx+6与x轴y轴分别交于点E/.F点E的坐标为(-8,0)点A的坐标为(-6.0)求K的 2020-07-13 …
如图,已知点A、B、C、D、E在同一直线上,且AC=BD,E是线段BC的中点.(1)点E是线段AD 2020-07-22 …
△ABC中,AB=AC=10,E是平面内一点,作∠EBC=∠BED=60,D在∠BAC平分线上,B 2020-07-31 …
如图,已知三角形abc,d在bc的延长线上,e在ca的的延长线上,f在ab的延长线上,试比较∠1与 2020-08-01 …
如图,在矩形ABCD中,AB=6,AD=23,E是AB边上一点,AE=2,F是直线CD上一动点,将△ 2020-11-02 …
1、灯A、B均标有220v,1000w字样,D、E是熔断器(D在火线上,E在插座C的线路上接火线)将 2020-11-07 …
已知椭圆E的中心在原点,焦点在x轴上,e=1/2,且E上一点到两焦点的距离之和为4.过椭圆E的左焦点 2020-11-22 …