已知函数f(x)＝＋xlnx(m>0)，g(x)＝lnx－2.(1)当m＝1时，求函数f(x)的单调增区间；(2)设函数h(x)＝f(x)－xg(x)－，x>0.若函数y＝h(h(x))的最小值是，求m的值；(3)若函数f(x)，g(x)的定义域

Question

已知函数f(x)＝＋xlnx(m>0)，g(x)＝lnx－2.

(1) 当m＝1时，求函数f(x)的单调增区间；

(2) 设函数h(x)＝f(x)－xg(x)－，x>0.若函数y＝h(h(x))的最小值是，求m的值；

(3) 若函数f(x)，g(x)的定义域都是，对于函数f(x)的图象上的任意一点A，在函数g(x)的图象上都存在一点B，使得OA⊥OB，其中e是自然对数的底数，0为坐标原点．求m的取值范围．

Answer 1

 (1) 当m＝1时，f(x)＝＋xlnx，

f′(x)＝－＋lnx＋1.(2分)

因为f′(x)在(0，＋∞)上单调增，且f′(1)＝0，

所以当x>1时，f′(x)>0；当0<x<1时，f′(x)<0.

所以函数f(x)的单调增区间是(1，＋∞)．(4分)

(2)

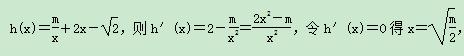
函数y＝h(h(x))的最小值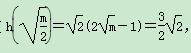

解得＝(舍)．

综上所述，m的值为1.(10分)

(3) 由题意知，k_OA＝＋lnx，k_OB＝.

考虑函数y＝，因为y′＝>0在上恒成立，

所以函数y＝在上单调增，故k_OB∈

所以k_OA∈，即≤＋lnx≤e在上恒成立，

即－x²lnx≤m≤x²(e－lnx)在上恒成立．

设p(x)＝－x²lnx，则p′(x)＝－2xlnx≤0在上恒成立，

所以p(x)在上单调减，所以m≥p(1)＝. (14分)

设q(x)＝x²(e－lnx)，

则q′(x)＝x(2e－1－2lnx)≥x(2e－1－2lne)>0在上恒成立，

所以q(x)在上单调增，所以m≤q(1)＝e.

综上所述，m的取值范围为

附加题