早教吧作业答案频道 -->数学-->
我们学习了锐角三角函数的相关知识,知道锐角三角函数定量地描述了在直角三角形中边角之间的联系.在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长的比与
题目详情
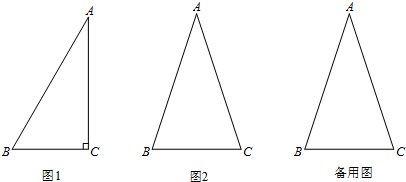
我们学习了锐角三角函数的相关知识,知道锐角三角函数定量地描述了在直角三角形中边角之间的联系.在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长的比与角的大小之间可以相互转化.如图1,在Rt△ABC中,∠C=90°.若∠A=30°,则cosA=
=
=
.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对.如图2,在△ABC中,AB=AC,顶角A的正对记作sadA,这时,sadA=
=
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述角的正对的定义,解答下列问题:
(1)直接写出sad60°的值为___;
(2)若0°<∠A<180°,则∠A的正对值sad A的取值范围是___;
(3)如图2,已知tanA=
,其中∠A为锐角,求sadA的值;
(4)直接写出sad36°的值为___.
| ∠A 的邻边 |
| 斜边 |
| AC |
| AB |
| ||
| 2 |
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对.如图2,在△ABC中,AB=AC,顶角A的正对记作sadA,这时,sadA=
| 底边 |
| 腰 |
| BC |
| AB |
根据上述角的正对的定义,解答下列问题:
(1)直接写出sad60°的值为___;
(2)若0°<∠A<180°,则∠A的正对值sad A的取值范围是___;
(3)如图2,已知tanA=
| 3 |
| 4 |
(4)直接写出sad36°的值为___.

▼优质解答
答案和解析
(1)根据正对定义,
当顶角为60°时,等腰三角形底角为60°,
则三角形为等边三角形,
则sad60°=
=1.
故答案为:1;
(2)当∠A接近0°时,sadA接近0,
当∠A接近180°时,等腰三角形的底接近于腰的二倍,故sadA接近2.
于是sadA的取值范围是0<sadA<2.
故答案为:0<sadA<2.
(3)如图2,过点B作BD⊥AC于点D.
∴∠ADB=∠CDB=90°.

在Rt△ADB中,tanA=
,
∴设BD=3k,则AD=4k.
∴AB=
=5k.
∵AB=AC,
∴CD=k.
∴在Rt△CDB中,利用勾股定理得,BC=
k.
在等腰△ABC中,sad A=
=
=
.
(4)如图3所示:已知:∠A=36°,AB=AC,BC=BD,
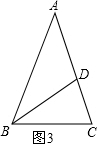
∴∠A=∠CBD=36°,∠ABC=∠C=72°,
∴△BCD∽△ABC,
∴
=
,
∴
=
,
解得:BC=
CD,
∴sad36°=
=
.
故答案为:
.
当顶角为60°时,等腰三角形底角为60°,
则三角形为等边三角形,
则sad60°=
| 1 |
| 1 |
故答案为:1;
(2)当∠A接近0°时,sadA接近0,
当∠A接近180°时,等腰三角形的底接近于腰的二倍,故sadA接近2.
于是sadA的取值范围是0<sadA<2.
故答案为:0<sadA<2.
(3)如图2,过点B作BD⊥AC于点D.
∴∠ADB=∠CDB=90°.

在Rt△ADB中,tanA=
| 3 |
| 4 |
∴设BD=3k,则AD=4k.
∴AB=
| BD2+AD2 |
∵AB=AC,
∴CD=k.
∴在Rt△CDB中,利用勾股定理得,BC=
| 10 |
在等腰△ABC中,sad A=
| BC |
| AB |
| ||
| 5k |
| ||
| 5 |
(4)如图3所示:已知:∠A=36°,AB=AC,BC=BD,

∴∠A=∠CBD=36°,∠ABC=∠C=72°,
∴△BCD∽△ABC,
∴
| BC |
| AC |
| CD |
| BC |
∴
| BC |
| BC+CD |
| CD |
| BC |
解得:BC=
| ||
| 2 |
∴sad36°=
| CD |
| BC |
| ||
| 2 |
故答案为:
| ||
| 2 |
看了 我们学习了锐角三角函数的相关...的网友还看了以下:
如图,Rt△ABC的锐角顶点是直线y=x+m与双曲线y=mx如图,Rt△ABC的锐角顶点是直线y= 2020-05-14 …
三角形的三个外角的度数之比为6:7:11,那么该三角形是()A一个内角为15°的锐角三角形B一个内 2020-05-23 …
一个直角三角形,其中一个锐角是另一个锐角的3倍,较大的锐角是()度,较小的锐角的()度要原因 2020-06-04 …
关于锐角三角函数的问题.我是预习下一学年的课程所以很多关于函数的都不清楚?tanA=角A的对边比上 2020-06-06 …
各位大虾··帮忙解小小的题—-—在Rt三角形ABC中,角C=90°,角A=30°,BC=2cm,则 2020-06-06 …
1,在一个直角三角形中,较小的锐角是较大锐角的三分之二,两个锐角分别是多少度?2,将一根长1米的圆 2020-06-15 …
四年纪数学题目直角三角形中,一个较大的锐角是较小的锐角的五倍,分别求出这两个锐角的度数,要简单易懂 2020-06-17 …
已知三角形的一角90度和两条边的长度,问它的锐是多少度.如题:直角90度边长,边高是问它的丫锐角多 2020-06-26 …
是否存在满足以下条件的锐角三角形ABC:其三边的长及一条高的长是四个连续的整数,且这条高将三角形A 2020-06-27 …
一个直角三角形,较小锐角的角度是较大的锐角的3分之2,这两个锐角分别是()度和()度 2020-07-03 …