如图，P为平行四边形ABCD边AD上一点，E、F分别是PB、PC（靠近点P）的三等分点，△PEF、△PDC、△PAB的面积分别为S1、S2、S3，若AD=2，AB=23，∠A=60°，则S1+S2+S3的值为（）A.103B.92C.133D.4

Question

如图，P为平行四边形ABCD边AD上一点，E、F分别是PB、PC（靠近点P）的三等分点，△PEF、△PDC、△PAB的面积分别为S₁、S₂、S₃，若AD=2，AB=2

√(3)，∠A=60°，则S₁+S₂+S₃的值为（　　）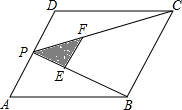

A.

(10)/(3)

B.

(9)/(2)

C.

(13)/(3)

D. 4

Answer 1

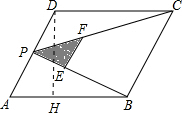作DH⊥AB于点H，如右图所示，
∵AD=2，AB=2√(3)，∠A=60°，
∴DH=AD•sin60°=2×(√(3))/(2)=√(3)，
∴S_▱ABCD=AB•DH=2√(3)•√(3)=6，
∴S₂+S₃=S_△PBC=3，
又∵E、F分别是PB、PC（靠近点P）的三等分点，
∴(S△PEF)/(S△PBC)=(1)/(9)，
∴S_△PEF=(1)/(9)×3=(1)/(3)，
即S₁=(1)/(3)，
∴S₁+S₂+S₃=(1)/(3)+3=(10)/(3)，
故选A．