早教吧作业答案频道 -->数学-->
如图,在O中,AC与BD是圆的直径,BE⊥AC,CF⊥BD,垂足分别为E、F(1)四边形ABCD是什么特殊的四边形?请判断并说明理由;(2)求证:BE=CF.
题目详情
如图,在 O中,AC与BD是圆的直径,BE⊥AC,CF⊥BD,垂足分别为E、F
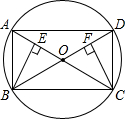
(1)四边形ABCD是什么特殊的四边形?请判断并说明理由;
(2)求证:BE=CF.

(1)四边形ABCD是什么特殊的四边形?请判断并说明理由;
(2)求证:BE=CF.
▼优质解答
答案和解析
(1) 四边形ABCD是矩形.理由如下:
∵AC与BD是圆的直径,
∴∠ABC=∠ADC=90°,∠BAD=∠BCD=90°,
∴四边形ABCD是矩形;
(2)证明:∵BO=CO,
又∵BE⊥AC于E,CF⊥BD于F,
∴∠BEO=∠CFO=90°.
在△BOE和△COF中,
,
∴△BOE≌△COF(AAS).
∴BE=CF.
∵AC与BD是圆的直径,
∴∠ABC=∠ADC=90°,∠BAD=∠BCD=90°,
∴四边形ABCD是矩形;
(2)证明:∵BO=CO,
又∵BE⊥AC于E,CF⊥BD于F,
∴∠BEO=∠CFO=90°.
在△BOE和△COF中,
|
∴△BOE≌△COF(AAS).
∴BE=CF.
看了 如图,在O中,AC与BD是圆...的网友还看了以下:
如图,OA=4,线段OA的中点为B,点C在圆O上AC叫圆O于D,且AD=CD求Bdad长如图,OA= 2020-03-31 …
八年级上册A、B两点分别位于一个池塘的两端,C为AD的中点,完成后续图形,使之能求出A、B的距离图 2020-05-13 …
梯形中,AO:0D=0.6,已知三角形ACO的面积的9平方厘米,求梯形ABCD的面积.图:A -- 2020-05-16 …
选出与所给单词划线部分读音相同的一项1、h(o)meA.c(o)meB.g(o)C.d(o)cto 2020-05-17 …
如图6所示,用两根绝缘丝线挂着两个质量相同不带电的小球A和B,此时,上、下丝线受的力分别为、;如果 2020-06-04 …
如图,AB为圆O的直径,PB为O的切线,AC//OP,点C在圆O上,OP交圆O于D,DA交BC于G 2020-06-27 …
有一个二次函数的题目,请各位帮帮我~~~~如图,已知抛物线的顶点为点A(3,2),且经过原点o,与 2020-06-27 …
四边形OABC是矩形,OA=4,OC=8,将矩形OABC沿直线Ac折叠四边形OABC是矩形,OA= 2020-07-26 …
如图,用尺规作图作“一个角等于已知角”的原理是:因为△D′O′C′≌△DOC,所以∠D′O′C′= 2020-07-31 …
(2014•丰南区二模)如图1,直径AC、BD将圆O四等分,动点P从圆心O出发,沿O→C→D→O路线 2020-12-20 …