早教吧作业答案频道 -->数学-->
如图,已知△ABC中,∠ABC=∠ACB,以点B为圆心,BC长为半径的弧分别交AC,AB于点D,E,连接BD,ED.(1)写出图中所有的等腰三角形;(2)若∠AED=114°,求∠ABD和∠ACB的度数.
题目详情
如图,已知△ABC中,∠ABC=∠ACB,以点B为圆心,BC长为半径的弧分别交AC,AB于点D,E,连接BD,ED.
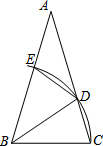
(1)写出图中所有的等腰三角形;
(2)若∠AED=114°,求∠ABD和∠ACB的度数.

(1)写出图中所有的等腰三角形;
(2)若∠AED=114°,求∠ABD和∠ACB的度数.
▼优质解答
答案和解析
(1)∵∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形;
∵BE=BD=BC,
∴△BCD,△BED是等腰三角形;
∴图中所有的等腰三角形有:△ABC,△BCD,△BED;
(2) ∵∠AED=114°,
∴∠BED=180°-∠AED=66°.
∵BD=BE,
∴∠BDE=∠BED=66°.
∴∠ABD=180°-66°×2=48°.
解法一:设∠ACB=x°,
∴∠ABC=∠ACB=x°.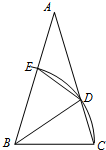
∴∠A=180°-2x°.
∵BC=BD,
∴∠BDC=∠ACB=x°.
又∵∠BDC为△ABD的外角,
∴∠BDC=∠A+∠ABD.
∴x=180-2x+48,解得:x=76.
∴∠ACB=76°.(10分)
解法二:设∠ACB=x°,
∴∠ABC=∠ACB=x°.
∴∠DBC=x°-48°.
∵BC=BD,
∴∠BDC=∠ACB=x°.
又∵∠DBC+∠BCD+∠BDC=180°,
∴x-48+x+x=180,解得:x=76.
∴∠ACB=76°.
∴AB=AC,
∴△ABC是等腰三角形;
∵BE=BD=BC,
∴△BCD,△BED是等腰三角形;
∴图中所有的等腰三角形有:△ABC,△BCD,△BED;
(2) ∵∠AED=114°,
∴∠BED=180°-∠AED=66°.
∵BD=BE,
∴∠BDE=∠BED=66°.
∴∠ABD=180°-66°×2=48°.
解法一:设∠ACB=x°,
∴∠ABC=∠ACB=x°.

∴∠A=180°-2x°.
∵BC=BD,
∴∠BDC=∠ACB=x°.
又∵∠BDC为△ABD的外角,
∴∠BDC=∠A+∠ABD.
∴x=180-2x+48,解得:x=76.
∴∠ACB=76°.(10分)
解法二:设∠ACB=x°,
∴∠ABC=∠ACB=x°.
∴∠DBC=x°-48°.
∵BC=BD,
∴∠BDC=∠ACB=x°.
又∵∠DBC+∠BCD+∠BDC=180°,
∴x-48+x+x=180,解得:x=76.
∴∠ACB=76°.
看了 如图,已知△ABC中,∠AB...的网友还看了以下:
直角三角形里有条和直角边平行的线,求这条线的长度直角三角形为ABC,其中AB、BC为直角边,直线D 2020-04-26 …
高二不等关系与基本不等式为处理含有某种杂质的污水要制作一个底宽为2米的无盖长方体沉淀箱,污水从A孔 2020-04-26 …
已知某厂生产量的月平均增长率为a(a>0)则该厂生产量的平均增长率为 2020-06-05 …
已知线段AB的长度为a,C是线段AB的中点,E、F分别是AC、CB的中点中点,求EF的长度,如果将 2020-06-15 …
1.直三棱柱ABC--A'B'C'中,各侧棱和底面的边长均为a,点D是侧棱CC'上任意一点,连接A 2020-06-27 …
如图,为处理含有某种杂质的污水,要制造一底宽为2米的无盖长方体沉淀箱,污水从A孔流入,经沉淀后从B 2020-07-11 …
已知三棱锥S-ABC中,有四条棱的长度都为2,另两条棱长都为a,则a的取值范围是? 2020-07-21 …
从小明的家到学校,是一段长度为a的上坡路接着一段长度为b的下坡路(两段路的长度不等,但坡度相同), 2020-07-30 …
如图所示,一根自然长度为l0的轻弹簧和一根长度为a的轻绳连接,弹簧的上端固定在天花板的O点上,P是 2020-07-31 …
已知三角形边长求高已知一个三角形(不是正三角形)的三边边长长度为a(a为底边长的长度)、b、c.求三 2020-11-04 …