早教吧作业答案频道 -->数学-->
感知:如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知:DB=DC.探究:如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.应用:如图③,四边形ABCD中,∠B=60°,∠C=120°,DB=DC=
题目详情
感知:如图①,AD平分∠BAC,∠B+∠C=180°,∠B=90°,易知:DB=DC.
探究:如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.
应用:如图③,四边形ABCD中,∠B=60°,∠C=120°,DB=DC=a,求AB-AC的值(用含a的代数式表示)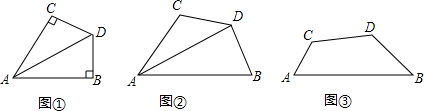
探究:如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.
应用:如图③,四边形ABCD中,∠B=60°,∠C=120°,DB=DC=a,求AB-AC的值(用含a的代数式表示)

▼优质解答
答案和解析
探究:证明:如图②中,DE⊥AB于E,DF⊥AC于F,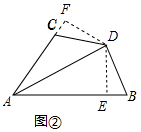
∵DA平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD,
在△DFC和△DEB中
,
∴△DFC≌△DEB(AAS),
∴DC=DB.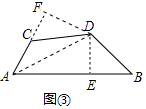
应用: 如图③连接AD、DE⊥AB于E,DF⊥AC于F,
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD,
在△DFC和△DEB中,
,
∴△DFC≌△DEB(AAS),
∴DF=DE,CF=BE,
在Rt△ADF和Rt△ADE中,
,
∴△RtADF≌Rt△ADE(HL),
∴AF=AE,
∴AB-AC=(AE+BE)-(AF-CF)=2BE,
在Rt△DEB中,∵∠DEB=90°,∠B=∠EDB=60°,BD=a,
∴∠BDE=30°,
∴BE=
BD=
a
∴AB-AC=2BE=a.

∵DA平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD,
在△DFC和△DEB中
|
∴△DFC≌△DEB(AAS),
∴DC=DB.

应用: 如图③连接AD、DE⊥AB于E,DF⊥AC于F,
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD,
在△DFC和△DEB中,
|
∴△DFC≌△DEB(AAS),
∴DF=DE,CF=BE,
在Rt△ADF和Rt△ADE中,
|
∴△RtADF≌Rt△ADE(HL),
∴AF=AE,
∴AB-AC=(AE+BE)-(AF-CF)=2BE,
在Rt△DEB中,∵∠DEB=90°,∠B=∠EDB=60°,BD=a,
∴∠BDE=30°,
∴BE=
| 1 |
| 2 |
| 1 |
| 2 |
∴AB-AC=2BE=a.
看了 感知:如图①,AD平分∠BA...的网友还看了以下:
三角形abc与三角形def完全相同.已知AB=8厘米,BE=5厘米,DH=3厘米.求梯形CHDF的 2020-05-13 …
已知|a|=8,b=6,a+b模=a-b模,则a-b的模=都是向量的模已知|a|=8,b=6,a+ 2020-05-14 …
数字信号处理题:x(n)是一实序列,知道8点的DFT为X(k),知道X(0)X(1)X(2)X(3 2020-05-17 …
1、求线段AB的长2、求线段AB的中线D表示的数3、已知AC=8,求x的值已知数轴上有A、B、C三 2020-06-03 …
338×9−3−0.375999×222+333×3341214-(1214-(325+2.25- 2020-06-14 …
如果8个人的平均年龄是48岁,已知在8人中,没有大于51岁的又知最多能有3人的年龄相同.那么年龄最 2020-06-19 …
已知数轴上有A,B,C三点,它们表示的有理数分别为6,-8,x.(1)求线段AB的长;(2)求线段 2020-07-14 …
````重赏!1.已知A(8,0),B(0,6)线段AB上的点P在X轴上的射影为Q(a,o),若三 2020-07-30 …
煤气收费规定,每月用量在8立方米或8立方米以下者一律收6.9元,超过每立方米按一定费用交费,某饭店1 2020-11-27 …
下列关于代数式未知数的平方—4倍的未知数+8的三个命题①该代数的式值必定大于8,②该代数式的值必定大 2021-01-01 …