早教吧作业答案频道 -->数学-->
如图,O的半径为1,A,P,B,C是O上的四个点.∠APC=∠CPB=60°.(1)判断△ABC的形状:;(2)当点P位于什么位置时,四边形APBC的面积最大?求出最大面积;(3)直接写出线段PA,PB,
题目详情
如图, O的半径为1,A,P,B,C是 O上的四个点.∠APC=∠CPB=60°.
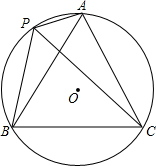
(1)判断△ABC的形状:___;
(2)当点P位于什么位置时,四边形APBC的面积最大?求出最大面积;
(3)直接写出线段PA,PB,PC之间的数量关系.

(1)判断△ABC的形状:___;
(2)当点P位于什么位置时,四边形APBC的面积最大?求出最大面积;
(3)直接写出线段PA,PB,PC之间的数量关系.
▼优质解答
答案和解析
证明:(1)△ABC是等边三角形.
证明如下:在 O中
∵∠BAC与∠CPB是
所对的圆周角,∠ABC与∠APC是
所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;
故答案为:等边三角形;
(2)当点P为
的中点时,四边形APBC的面积最大.
理由如下,如图2,过点P作PE⊥AB,垂足为E.
过点C作CF⊥AB,垂足为F.
∵S△APB=
AB•PE,S△ABC=
AB•CF,
∴S四边形APBC=
AB•(PE+CF),
当点P为
的中点时,PE+CF=PC,PC为 O的直径,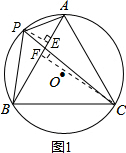
∴此时四边形APBC的面积最大.
又∵ O的半径为1,
∴其内接正三角形的边长AB=
,
∴S四边形APBC=
×2×
=
;
(3)在PC上截取PD=AP,如图2,
又∵∠APC=60°,
∴△APD是等边三角形,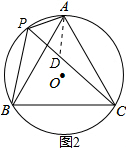
∴AD=AP=PD,∠ADP=60°,即∠ADC=120°.
又∵∠APB=∠APC+∠BPC=120°,
∴∠ADC=∠APB,
在△APB和△ADC中,
,
∴△APB≌△ADC(AAS),
∴BP=CD,
又∵PD=AP,
∴CP=BP+AP.
证明如下:在 O中
∵∠BAC与∠CPB是
 |
| BC |
 |
| AC |
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;
故答案为:等边三角形;
(2)当点P为
 |
| AB |
理由如下,如图2,过点P作PE⊥AB,垂足为E.
过点C作CF⊥AB,垂足为F.
∵S△APB=
| 1 |
| 2 |
| 1 |
| 2 |
∴S四边形APBC=
| 1 |
| 2 |
当点P为
 |
| AB |

∴此时四边形APBC的面积最大.
又∵ O的半径为1,
∴其内接正三角形的边长AB=
| 3 |
∴S四边形APBC=
| 1 |
| 2 |
| 3 |
| 3 |
(3)在PC上截取PD=AP,如图2,
又∵∠APC=60°,
∴△APD是等边三角形,

∴AD=AP=PD,∠ADP=60°,即∠ADC=120°.
又∵∠APB=∠APC+∠BPC=120°,
∴∠ADC=∠APB,
在△APB和△ADC中,
|
∴△APB≌△ADC(AAS),
∴BP=CD,
又∵PD=AP,
∴CP=BP+AP.
看了 如图,O的半径为1,A,P,...的网友还看了以下:
o为等边三角形abc的中心,射线oe交ab于点e,of交bc于点f.若三角形abc面积为s∠eof 2020-04-11 …
已知一次函数y=kx+b的图象经过点A(3,0),与y轴交于点B,若△AOB的面积为6,试求点B的 2020-06-14 …
当x=0时怎么确定∫(积分上限为x积分下线为0)f(t)dt的定义域中包括x=0设f(x)是奇函数 2020-06-26 …
零点的太阳高度怎么求某地(70°N,60°E),当地0点时,太阳高度是多少?请问怎么求呐、?那天是 2020-06-28 …
平面向量三角解题已知向量OA的模=1,向量OB的模=√3(即根号3),OA的模与OB的模的乘积=0 2020-07-07 …
已知面积S,S内有很~多个点.点间间距0.5M.求面积S内最多有多少个点.例如1平米的地方内有9个 2020-07-10 …
f(x)为分段函数,当x≠0时,f(x)=1/x,当x=0时,f(x)=0,这个函数是否存在不定积 2020-07-20 …
当x=0时,y=-1,即B点的坐标是(0,-1)当y=0时,x=2,即A点的坐标是(2,0)为什么 2020-07-30 …
已知三角形AOC,点O(0,0),点C(4,0),点A在直线y=-x+3的图像上已知三角形AOC, 2020-07-30 …
一个展厅用方砖铺地,用面积0点36平方米的方砖需要3000块.如果改用边长5分米,需要多少块? 2020-12-24 …