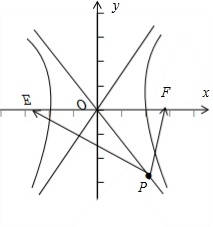
已知点P（3，-4）是双曲线x2a2-y2b2=1(a>0，b>0)渐近线上的一点，E，F是左，右两个焦点，若EP•FP=0，则双曲线方程为（）A.x218-y232=1B.x232-y218=1C.x29-y216=1D.x216-y29=1

Question

已知点P（3，-4）是双曲线

(x2)/(a2)-(y2)/(b2)=1(a>0，b>0)渐近线上的一点，E，F是左，右两个焦点，若

EP

•

FP

=0，则双曲线方程为（　　）

A.

(x2)/(18)-(y2)/(32)=1

B.

(x2)/(32)-(y2)/(18)=1

C.

(x2)/(9)-(y2)/(16)=1

D.

(x2)/(16)-(y2)/(9)=1

Answer 1

由题意可得点P（3，-4）是双曲线(x2)/(a2)-(y2)/(b2)=1(a>0，b>0)渐近线上的一点，可得4a=3b，
因为E，F分别是双曲线的左、右焦点，故E（-c，0），F（c，0），

EP

•

FP

=0，
故c²=25，
又a²+b²=c²=25，结合4a=3b可解得a=3，b=4，
故双曲线的方程为：(x2)/(9)-(y2)/(16)=1．
故选：C．