早教吧作业答案频道 -->数学-->
如图,在△ABC中,已知点D在BC边上,AD•sin∠C+AC•sin∠ADC=DC•sin∠DAC,sin∠BAC=223,AB=32,AD=3.(1)求证:△ADC是直角三角形;(2)求△ABD的面积及BD的长.
题目详情
如图,在△ABC中,已知点D在BC边上,AD•sin∠C+AC•sin∠ADC=DC•sin∠DAC,sin∠BAC=
,AB=3
,AD=3.
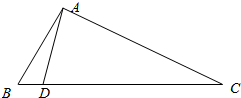
(1)求证:△ADC是直角三角形;
(2)求△ABD的面积及BD的长.
2
| ||
| 3 |
| 2 |

(1)求证:△ADC是直角三角形;
(2)求△ABD的面积及BD的长.
▼优质解答
答案和解析
(1)证明:∵点D在BC边上,AD•sin∠C+AC•sin∠ADC=DC•sin∠DAC,
由正弦定理可得:AD2+AC2=DC2,
∴∠DAC=90°.
∴△ADC是直角三角形.
(2) ∵sin∠BAC=
=sin(∠BAD+90°)=cos∠BAD,
又∠BAD是锐角,∴sin∠BAD=
=
.
∴S△BAD=
AB•AD•sin∠BAD=
×3
×3×
=
.
由余弦定理可得:BD2=(3
)2+32-2×3
×3×cos∠BAD=3,
解得BD=
.
由正弦定理可得:AD2+AC2=DC2,
∴∠DAC=90°.
∴△ADC是直角三角形.
(2) ∵sin∠BAC=
2
| ||
| 3 |
又∠BAD是锐角,∴sin∠BAD=
| 1-cos2∠BAD |
| 1 |
| 3 |
∴S△BAD=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 3 |
3
| ||
| 2 |
由余弦定理可得:BD2=(3
| 2 |
| 2 |
解得BD=
| 3 |
看了 如图,在△ABC中,已知点D...的网友还看了以下:
设点A,B是反比例函数y=−2x的图象上关于原点对称的两点,AD平行于y轴交x轴于点D,BC平行于 2020-04-08 …
设栈S的初始状态为空,元素a,b,c,d,e,f依次入栈S,出栈的序列为b,d,f,e,c,a…… 2020-05-17 …
地震波横波(S)和纵波(P)的传播速度在莫霍面处发生的显著变化是()A.S波、P波都明显增加B.S 2020-07-10 …
已知a,b,c,d都是正数,S=ab+c+d+ba+c+d+ca+b+d+da+b+c,则有()A 2020-07-30 …
如果棱台的两底面积分别是S,S′,中截面的面积是S,那么()A.2B.S=C.2S=S+S′D.S 2020-07-31 …
一条磁铁从中间折成两段后()A.S极的那一半只有S极,N极的那一半只有N极B.两半都有N极和S极C. 2020-11-01 …
C语言简单小问题已知s是字符型变量,下面正确的赋值语句是()。A.s=’abc’;B.s=’\08’ 2020-11-07 …
(1999•南通)溶解度为S克的某物质的饱和溶液,跟水以1:4的质量比混合后,溶液的质量百分比浓度为 2020-11-12 …
在古登堡面,横波(S)和纵波(P)传播速度的显著变化表现为A.S、P都明显增大B.S完全消失,P突然 2020-12-15 …
在古登堡界面,横波(S)和纵波(P)传播速度的显著变化表现为()A.S、P都明显增大B.S完全消失, 2020-12-15 …