早教吧作业答案频道 -->数学-->
如图，已知⊙O为四边形ABCD的外接圆，O为圆心，若∠BCD=120°，AB=AD=2，则⊙O的半径长为（）A.322B.62C.32D.233
题目详情
如图，已知⊙O为四边形ABCD的外接圆，O为圆心，若∠BCD=120°，AB=AD=2，则⊙O的半径长为（ ）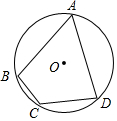
A. 3 2 2
B. 6 2
C. 3 2
D. 2 3 3
▼优质解答
答案和解析
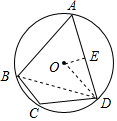连接BD，作OE⊥AD，连接OD，
∵⊙O为四边形ABCD的外接圆，∠BCD=120°，
∴∠BAD=60°．
∵AD=AB=2，
∴△ABD是等边三角形．
∴DE=
AD=1，∠ODE=
∠ADB=30°，
∴OD=
=
．
故选D．
连接BD，作OE⊥AD，连接OD，∵⊙O为四边形ABCD的外接圆，∠BCD=120°，
∴∠BAD=60°．
∵AD=AB=2，
∴△ABD是等边三角形．
∴DE=
| 1 |
| 2 |
| 1 |
| 2 |
∴OD=
| DE |
| cos30° |
2
| ||
| 3 |
故选D．
看了 如图，已知⊙O为四边形ABC...的网友还看了以下：
下图中的图A为某生物体细胞有丝分裂示意图,图B表示在一个细胞周期(G.、S、@组成若图A所示细胞来 2020-04-06 …
1.如果f(x)=(1/1+x^2)+x^2*∫^∧1∨0f(x)dx,求∫∧1∨0f(x)dx的 2020-04-13 …
一元二次方程的根的算式a为方程x^2-3x-1=0的根,求a^2除以(a^+a^2+1)的值.a为 2020-04-26 …
根据三角形的三边关系,判断下列四组线段中一定能组成三角形的是A：3,4,5B:3+a,4+a,5+ 2020-05-13 …
在水平桌面M上放置一块正方形薄木板abcd，在木板的正中点放里一个质量为m的木块，如图所示．先以木 2020-05-17 …
微分方程y"+y'=2x^2e^x的特解应设为y*=A.(Ax^2+Bx+C)e^xB.(Ax^3 2020-05-22 …
设3*3矩阵A=a11,1a1,11a,问A为满秩矩阵时,a的值,a为多少时,r(A) 2020-06-12 …
已知ABC的坐标分别为A（3,0）B（0,3）C（cosa,sina）a属于（派/2,3派/2）1 2020-07-08 …
|2E+A²|的特征值是怎么求出来的?题目是这样的：A为二阶矩阵,每行元素之和为4,|E+A|=0 2020-07-13 …
|2E+A²|的特征值是怎么求出来的?题目是这样的：A为二阶矩阵,每行元素之和为4,|E+A|=0 2020-07-18 …