早教吧作业答案频道 -->数学-->
(1)如图①,四边形ABCD是正方形,点G是BC上的任意一点,BF⊥AG于点F,DE⊥AG于点E,探究BF,DE,EF之间的数量关系,第一学习小组合作探究后,得到DE-BF=EF,请证明这个结论;(2)若(1)中
题目详情
(1)如图①,四边形ABCD是正方形,点G是BC上的任意一点,BF⊥AG于点F,DE⊥AG于点E,探究BF,DE,EF之间的数量关系,第一学习小组合作探究后,得到DE-BF=EF,请证明这个结论;
(2)若(1)中的点G在CB的延长线上,其余条件不变,请在图②中画出图形,并直接写出此时BF,DE,EF之间的数量关系;
(3)如图③,四边形ABCD内接于 O,AB=AD,E,F是AC上的两点,且满足∠AED=∠BFA=∠BCD,试判断AC,DE,BF之间的数量关系,并说明理由.
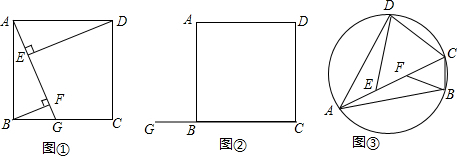
(2)若(1)中的点G在CB的延长线上,其余条件不变,请在图②中画出图形,并直接写出此时BF,DE,EF之间的数量关系;
(3)如图③,四边形ABCD内接于 O,AB=AD,E,F是AC上的两点,且满足∠AED=∠BFA=∠BCD,试判断AC,DE,BF之间的数量关系,并说明理由.

▼优质解答
答案和解析
(1)如图1中,结论:DE-BF=EF.理由如下:
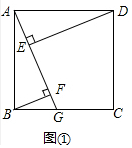
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵BF⊥AG于点F,DE⊥AG于点E,
∴∠AFB=∠DEA=90°,
∵∠BAF+∠DAE=90°,∠DAE+∠ADE=90°,
∴∠BAF=∠ADE,
在△ABF和△DAE中,
,
∴△ABF≌△DAE,
∴BF=AE,AF=DE,
∵AF-AE=EF,
∴DE-BF=EF.
(2)结论EF=DE+BF.理由如下:
如图2中,
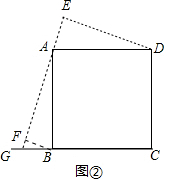
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵BF⊥AG于点F,DE⊥AG于点E,
∴∠AFB=∠DEA=90°,
∵∠BAF+∠DAE=90°,∠DAE+∠ADE=90°,
∴∠BAF=∠ADE,
在△ABF和△DAE中,
,
∴△ABF≌△DAE,
∴BF=AE,AF=DE,
∴EF=AF+AF=DE+BF.
(3)如图3中,结论:AC=BF+DE.理由如下:
连接BD.
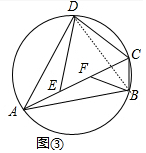
∵∠DBC+∠BDC+∠DCB=180°,∠DAE+∠ADE+∠AED=180°,
又∵∠DBC=∠DAE,∠DCB=∠AED,
∴∠ADE=∠BDC,
∵∠BDC=∠BAF,
∴∠ADE=∠BAF,∵AD=AB,∠AED=∠AFB,
∴△ADE≌△BAF,
∴AE=BF,
∵AD=AB,
∴∠ADB=∠ABD=∠ACD,
∵∠ADE=∠CDB,
∴∠CDE=∠ADB,
∴∠EDC=∠ECD,
∴DE=CE,
∴AC=BF+DE.

∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵BF⊥AG于点F,DE⊥AG于点E,
∴∠AFB=∠DEA=90°,
∵∠BAF+∠DAE=90°,∠DAE+∠ADE=90°,
∴∠BAF=∠ADE,
在△ABF和△DAE中,
|
∴△ABF≌△DAE,
∴BF=AE,AF=DE,
∵AF-AE=EF,
∴DE-BF=EF.
(2)结论EF=DE+BF.理由如下:
如图2中,

∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∵BF⊥AG于点F,DE⊥AG于点E,
∴∠AFB=∠DEA=90°,
∵∠BAF+∠DAE=90°,∠DAE+∠ADE=90°,
∴∠BAF=∠ADE,
在△ABF和△DAE中,
|
∴△ABF≌△DAE,
∴BF=AE,AF=DE,
∴EF=AF+AF=DE+BF.
(3)如图3中,结论:AC=BF+DE.理由如下:
连接BD.

∵∠DBC+∠BDC+∠DCB=180°,∠DAE+∠ADE+∠AED=180°,
又∵∠DBC=∠DAE,∠DCB=∠AED,
∴∠ADE=∠BDC,
∵∠BDC=∠BAF,
∴∠ADE=∠BAF,∵AD=AB,∠AED=∠AFB,
∴△ADE≌△BAF,
∴AE=BF,
∵AD=AB,
∴∠ADB=∠ABD=∠ACD,
∵∠ADE=∠CDB,
∴∠CDE=∠ADB,
∴∠EDC=∠ECD,
∴DE=CE,
∴AC=BF+DE.
看了 (1)如图①,四边形ABCD...的网友还看了以下:
用细绳栓住一小球,手拉着绳子使小球在水平桌面上滑动,此时小球受到的摩擦力大小是f,若让小球在该水平 2020-05-02 …
已知f(x)=ax^3+cx+d(a不等于0)是R上的奇函数,当x=1是f(x)取得极值负二.求f 2020-06-06 …
已知两个力,物体平衡,求第三个力最小值一小球用轻绳悬于O点,用力F拉住小球,使悬线保持偏离竖直方向 2020-06-15 …
如图所示,用轻绳吊一个重为G的小球,欲施一力F使小球在图示位置平衡(θ<30°),下列说法正确的是 2020-07-14 …
在光滑水平面上有一小车A,质量m=2kg,小车上放一个物体B,质量m=1kg,给B一个水平推力F, 2020-07-15 …
如图为一小球从A点沿直线运动到F点的频闪照片,若频闪照相机每隔0.2s闪拍一次,分析照片可知:小球 2020-07-20 …
将悬浮在水中的马铃薯切去一小块后再放回水中,重新静止时马铃薯所处的浮沉情况及马铃薯切去前后所受浮力F 2020-10-29 …
若f(小)在(-9,9)内可微,且f′(0)=0,f″(0)=A存在,则极限li5小→0f(小)−f 2020-11-03 …
(2014•安顺)如图是一小球从A点沿直线运动到F点的频闪照片,若频闪照相机每隔0.2s闪拍一次,分 2020-11-13 …
高一函数f(x)是定义在(0,-∞)上的增函数,且f(x/y)=f(x)-f(y),(1)求f(1) 2020-11-18 …