早教吧作业答案频道 -->数学-->
在棱长为1的正方体ABCD-A'B'C'D'中,E是AA'的中点,P是三角形BDC'内的动点,EP⊥BC',则P的轨迹长为()A.22B.32C.324D.64
题目详情
在棱长为1的正方体ABCD-A'B'C'D'中,E是AA'的中点,P是三角形BDC'内的动点,EP⊥BC',则P的轨迹长为( )
A. 2 2
B. 3 2
C. 3 2 4
D. 6 4
▼优质解答
答案和解析
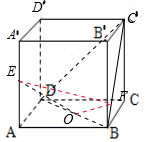 在棱长为1的正方体ABCD-A'B'C'D'中,E是AA'的中点,取BD的中点O,连接EO,因为A′C⊥平面BDC',可知EO⊥BC',则O就是P轨迹上的一个点,作OF⊥BC',于F,可得BC'⊥平面EFO,所以P在OF上,OF的长就是P的轨迹长.
在棱长为1的正方体ABCD-A'B'C'D'中,E是AA'的中点,取BD的中点O,连接EO,因为A′C⊥平面BDC',可知EO⊥BC',则O就是P轨迹上的一个点,作OF⊥BC',于F,可得BC'⊥平面EFO,所以P在OF上,OF的长就是P的轨迹长.
因为正方体的棱长为1,所以BD=
,则OF=
×
×
=
.
故选:D.
 在棱长为1的正方体ABCD-A'B'C'D'中,E是AA'的中点,取BD的中点O,连接EO,因为A′C⊥平面BDC',可知EO⊥BC',则O就是P轨迹上的一个点,作OF⊥BC',于F,可得BC'⊥平面EFO,所以P在OF上,OF的长就是P的轨迹长.
在棱长为1的正方体ABCD-A'B'C'D'中,E是AA'的中点,取BD的中点O,连接EO,因为A′C⊥平面BDC',可知EO⊥BC',则O就是P轨迹上的一个点,作OF⊥BC',于F,可得BC'⊥平面EFO,所以P在OF上,OF的长就是P的轨迹长.因为正方体的棱长为1,所以BD=
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 2 |
| ||
| 4 |
故选:D.
看了 在棱长为1的正方体ABCD-...的网友还看了以下:
理在事先是什么观点?7.下列观点中属于客观唯心主义观点的是()A.“吾心即是宇宙,宇宙即是吾心”B 2020-04-06 …
全概率公式?P(A)=P(A|B)*P(B)+P(A|否B)*P(否B),为什么不是这样的P(A) 2020-04-25 …
境界线上的地平线中的P.A.Oda,K.P.A.Italy,三征西班牙,六护式法兰西的意义 2020-05-16 …
在平面直角坐标系中,抛物线y=经过A(-1,0)B(3,0)C(0,-1)在平面直角坐标系中,抛物 2020-05-16 …
在平面直角坐标系中,抛物线经过A(-1,0)B(3,0)C(0,-1)三点,点Q在Y轴上,点 P在 2020-05-16 …
某公司的年销额为A元,成本为销售额的 60%,税额和其他费用合计为销售额的P%.a等于8000万, 2020-05-17 …
在极坐标系中,下列点与点M(1,2派\3)为同一点的是A(-1,派/3)B(1,-派/3)C(-1 2020-05-17 …
不是分组交换特点的是A.节点暂时存储的是一个个分组,而不是整个数据文件B.分组是暂时保存在节点 2020-05-24 …
不是分组变换特点的是A.节点暂时存储的是一个个分组,而不是整个数据文件B.分组是暂时保存在节点 2020-05-24 …
大断面岸上部分资料整理、计算成果数据为各地形点的()。A、起点距及高程B、水平距离C、高程D、起点 2020-05-27 …