早教吧作业答案频道 -->数学-->
如图①,平面直角坐标系XOY中,若A(0,a)、B(b,0)且(a-4)2+b-1=0,以AB为直角边作等腰Rt△ABC,∠CAB=90°,AB=AC.(1)求C点坐标;(2)如图②过C点作CD
题目详情
如图①,平面直角坐标系XOY中,若A(0,a)、B(b,0)且(a-4)2+
=0,以AB为直角边作等腰Rt△ABC,∠CAB=90°,AB=AC.
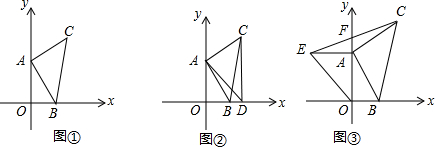
(1)求C点坐标;
(2)如图②过C点作CD⊥X轴于D,连接AD,求∠ADC的度数;
(3)如图③在(1)中,点A在Y轴上运动,以OA为直角边作等腰Rt△OAE,连接EC,交Y轴于F,试问A点在运动过程中S△AOB:S△AEF的值是否会发生变化?如果没有变化,请直接写出它们的比值___(不需要解答过程或说明理由).
| | b-1 |

(1)求C点坐标;
(2)如图②过C点作CD⊥X轴于D,连接AD,求∠ADC的度数;
(3)如图③在(1)中,点A在Y轴上运动,以OA为直角边作等腰Rt△OAE,连接EC,交Y轴于F,试问A点在运动过程中S△AOB:S△AEF的值是否会发生变化?如果没有变化,请直接写出它们的比值___(不需要解答过程或说明理由).
▼优质解答
答案和解析
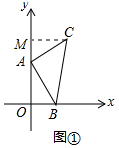 (1)作CM⊥OA于M,如图①所示:
(1)作CM⊥OA于M,如图①所示:
则∠CMA=∠AOB=90°,
∴∠OAB+∠ABO=90°,
∵(a-4)2+
=0,
∴a-4=0,b-1=0,
∴a=4,b=1,
∴OA=4,OB=1,
∵∠CAB=90°,
∴∠OAB+∠CAM=90°,
∴∠CAM=∠ABO,
在△CAM和△ABO中,
,
∴△CAM≌△ABO(AAS),
∴MC=OA=4,MA=OB=1,
∴OM=OA+MA=5,
∴C点坐标为(4,5);
(2)∵CD⊥x轴,∴D(4,0),
∴OD=OA,
∴△OAD为等腰直角三角形,
∴∠ADO=45°,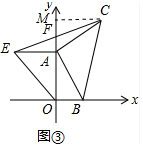
∴∠ADC=90°-45°=45°;
(3)A点在运动过程中S△AOB:S△AEF的值不会发生变化,S△AOB:S△AEF=2;理由如下:
作CM⊥OA于M,如图③所示:
同(1)得:△CAM≌△ABO,
∴MC=OA=a,MA=OB=b,
∴C点坐标为(a,a+b),
∵△OAE是等腰直角三角形,
∴AE=OA=a,
∴E(-a,a),
设直线CE的解析式为y=kx+c,
把点C和E的坐标代入得:
,
解得:
,
当x=0时,y=
,
∴F(0,
),
∴OF=
,
∴AF=OF-OA=
,
∵S△AOB=
ab,
S△AEF=
a×
b=
 (1)作CM⊥OA于M,如图①所示:
(1)作CM⊥OA于M,如图①所示:则∠CMA=∠AOB=90°,
∴∠OAB+∠ABO=90°,
∵(a-4)2+
| b-1 |
∴a-4=0,b-1=0,
∴a=4,b=1,
∴OA=4,OB=1,
∵∠CAB=90°,
∴∠OAB+∠CAM=90°,
∴∠CAM=∠ABO,
在△CAM和△ABO中,
|
∴△CAM≌△ABO(AAS),
∴MC=OA=4,MA=OB=1,
∴OM=OA+MA=5,
∴C点坐标为(4,5);
(2)∵CD⊥x轴,∴D(4,0),
∴OD=OA,
∴△OAD为等腰直角三角形,
∴∠ADO=45°,

∴∠ADC=90°-45°=45°;
(3)A点在运动过程中S△AOB:S△AEF的值不会发生变化,S△AOB:S△AEF=2;理由如下:
作CM⊥OA于M,如图③所示:
同(1)得:△CAM≌△ABO,
∴MC=OA=a,MA=OB=b,
∴C点坐标为(a,a+b),
∵△OAE是等腰直角三角形,
∴AE=OA=a,
∴E(-a,a),
设直线CE的解析式为y=kx+c,
把点C和E的坐标代入得:
|
解得:
|
当x=0时,y=
| 2a+b |
| 2 |
∴F(0,
| 2a+b |
| 2 |
∴OF=
| 2a+b |
| 2 |
∴AF=OF-OA=
| b |
| 2 |
∵S△AOB=
| 1 |
| 2 |
S△AEF=
| 1 |
| 2 |
| 1 |
| 2 |
|
作业帮用户
2018-01-21
|
看了 如图①,平面直角坐标系XOY...的网友还看了以下:
1、已知a,b,c互不相等求2a-b-c/(a-b)(b-c)+2b-c-a/(b-c)(b-a) 2020-05-16 …
求教分析一道代数式值题的解答过程.题目是这样的:已知(b+c)/a=(a+c)/b=(a+b)/c 2020-05-20 …
4.化简(m-c)/[(m-a)(m-b)]+(b-c)/[(a-b)(m-b)]+(b-c)/[ 2020-05-21 …
1.m-mmX=3+1,y=9+(1/3),试求y与x的函数关系式2.已知:a+x方=2005,b 2020-06-03 …
已知有理数a.b.c.在数轴上的位置如图所示,|a|=|b|1.a+b与a/b的值;2.c-a/c 2020-06-03 …
已知a+b+c=0,试求a^2/(2a^2+bc)+b^2/(2b^2+ac)+c^2/(2c^2 2020-06-11 …
1.已知a,b,c∈R.a+b+c=1a²+b²+c²=1/2求证c≥02(1)已知a,c是正实数 2020-07-14 …
若用A、B、C、分别表示有理数a、b、c,0为原点,如图所示.已知a<c<0,b>0.(1)化简| 2020-07-21 …
高二数学题,帮忙解决,要步骤的(1)设a,b,c属于R,a+b+c=0,abc0.(2)设a,b, 2020-07-22 …
判断下列命题的真假已知a,b,c,d∈R(1)若ac>bc,则a>b(2)若a>-b,则c-ab>c 2020-12-13 …
 扫描下载二维码
扫描下载二维码