某湿地公园内有一条河，现打算建一座桥（如图1）将河两岸的路连接起来，剖面设计图纸（图2）如下，其中，点A，E为x轴上关于原点对称的两点，曲线段BCD是桥的主体，C为桥顶，并且曲线

Question

某湿地公园内有一条河，现打算建一座桥（如图1）将河两岸的路连接起来，剖面设计图纸（图2）如下，

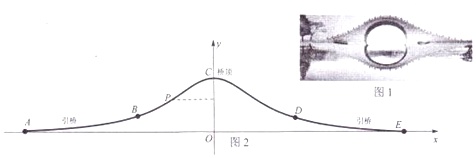
其中，点A，E为x轴上关于原点对称的两点，曲线段BCD是桥的主体，C为桥顶，并且曲线段BCD在图纸上的图形对应函数的解析式为y=(8)/(4+x2)（x∈[-2，2]），曲线段AB，DE均为开口向上的抛物线段，且A，E分别为两抛物线的顶点．设计时要求：保持两曲线在各衔接处（B，D）的切线的斜率相等．
（1）曲线段AB在图纸上对应函数的解析式，并写出定义域；
（2）车辆从A经B到C爬坡，定义车辆上桥过程中某点P所需要的爬坡能力为：M=（该点P与桥顶间的水平距离）×（设计图纸上该点P处的切线的斜率）其中M_P的单位：米．若该景区可提供三种类型的观光车：①游客踏乘；②蓄电池动力；③内燃机动力，它们的爬坡能力分别为0.8米，1.5米，2.0米，用已知图纸上一个单位长度表示实际长度1米，试问三种类型的观光车是否都可以顺利过桥？

Answer 1

（1）由题意A为抛物线的顶点，设A（a，0）（a<-2），则可设方程为y=λ（x-a）²（a≤x≤-2，λ>0），y′=2λ（x-a）．
曲线段BCD在图纸上的图形对应函数的解析式为y=(8)/(4+x2)（x∈[-2，2]），
y′=(-16x)/((4+x2)2)，且B（-2，1），则曲线在B处的切线斜率为(1)/(2)，
∴

λ(-2-a)2=1

2λ(-2-a)=(1)/(2)

，∴a=-6，λ=(1)/(16)，
∴曲线段AB在图纸上对应函数的解析式为y=(1)/(16)(x+6)2（-6≤x≤-2）；
（2）设P为曲线段AC上任意一点．
①P在曲线段AB上，则通过该点所需要的爬坡能力（M_P）₁=(-x)•(1)/(8)(x+6)=-(1)/(8)[(x+3)2-9]，
在[-6，-3]上为增函数，[-3，-2]上是减函数，最大为(9)/(8)米；
②P在曲线段BC上，则通过该点所需要的爬坡能力（M_P）₂=(-x)•(-16x)/((4+x2)2)=(16x2)/((4+x2)2)（x∈[-2，0]），
设t=x²，t∈[0，4]，（M_P）₂=y=(16t)/((4+t)2)．
t=0，y=0；0<t≤4，y=(16)/((16)/(t)+t+8)≤1（t=4取等号），此时最大为1米．
由上可得，最大爬坡能力为(9)/(8)米；
∵0.8<(9)/(8)<1.5<2，
∴游客踏乘不能顺利通过该桥；蓄电池动力和内燃机动力能顺利通过该桥．