早教吧作业答案频道 -->数学-->
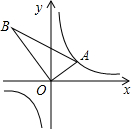
如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=1x的图象上.若点B在反比例函数y=kx的图象上,则k的值为.
题目详情
如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=
的图象上.若点B在反比例函数y=
的图象上,则k的值为___.
| 1 |
| x |
| k |
| x |

▼优质解答
答案和解析
过点A,B作AC⊥x轴,BD⊥x轴,分别于C,D.
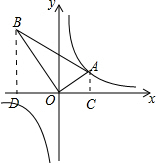
设点A的坐标是(m,n),则AC=n,OC=m.
∵∠AOB=90°,
∴∠AOC+∠BOD=90°.
∵∠DBO+∠BOD=90°,
∴∠DBO=∠AOC.
∵∠BDO=∠ACO=90°,
∴△BDO∽△OCA.
∴
=
=
.
∵OB=2OA,
∴BD=2m,OD=2n.
因为点A在反比例函数y=
的图象上,
∴mn=1.
∵点B在反比例函数y=
的图象上,
∴B点的坐标是(-2n,2m).
∴k=-2n•2m=-4mn=-4.
故答案为:-4.

设点A的坐标是(m,n),则AC=n,OC=m.
∵∠AOB=90°,
∴∠AOC+∠BOD=90°.
∵∠DBO+∠BOD=90°,
∴∠DBO=∠AOC.
∵∠BDO=∠ACO=90°,
∴△BDO∽△OCA.
∴
| BD |
| OC |
| OD |
| AC |
| OB |
| OA |
∵OB=2OA,
∴BD=2m,OD=2n.
因为点A在反比例函数y=
| 1 |
| x |
∴mn=1.
∵点B在反比例函数y=
| k |
| x |
∴B点的坐标是(-2n,2m).
∴k=-2n•2m=-4mn=-4.
故答案为:-4.
看了 如图,△AOB是直角三角形,...的网友还看了以下:
如图1抛物线y=ax2+bx+c经过点A(-1,0)且经过直线y=x-3与x轴的交点b与y轴的交点 2020-05-13 …
如图 已知 直线l∶y=-√3x÷3+√3交x轴于点A 交y轴于点B 将△AOB沿直线l翻折 点如 2020-05-16 …
高二数学麻烦了等可能的取点p(x,y),其中x∈[-3,3],y∈[0,3]1、当X∈Z,Y∈Z时 2020-06-10 …
求下列各点的坐标,并将各点标在直角坐标系中.(1)点A在y轴上,且在x轴上方,距离原点5个单位;( 2020-06-14 …
随机取点P(x,y),其中0小于等于x小于等于4,0小于等于y小于等于4.)(1)求当x,y属于Z 2020-06-27 …
如图,在平面直角坐标系中,O为坐标原点,P(x,y),PA⊥x轴于点A,PB⊥y轴于点B,C(a, 2020-07-21 …
点p(x,y)的横、纵坐标x、y满足xy<0且x>y则点(-1,m²+1)一定在A第一象限B第二象 2020-08-01 …
反比例函数y=ax(a>0,a为常数)和y=2x在第一象限内的图象如图所示,点M在y=ax的图象上 2020-08-03 …
如左图:直线y=kx+4k(k≠0)交x轴于点A,交y轴于点C,点M(2,m)为直线AC上一点,过点 2020-11-01 …
求y^2=2px(p>0)的参数方程1以抛物线上一点(x,y)与顶点连线斜率的倒求y^2=2px(p 2021-01-22 …