早教吧作业答案频道 -->数学-->
在边长为2的正三角形ABC内任取一点P，则使点P到三个顶点的距离都不小于1的概率是．
题目详情
在边长为2的正三角形ABC内任取一点P，则使点P到三个顶点的距离都不小于1的概率是___．
▼优质解答
答案和解析
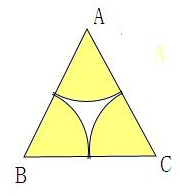满足条件的正三角形ABC如下图所示：
其中正三角形ABC的面积S三角形=
×4=
．
满足到正三角形ABC的顶点A、B、C的距离至少有一个小于1的平面区域如图中阴影部分所示，其加起来是一个半径为1的半圆，
则S阴影=
π，
则使取到的点到三个顶点A、B、C的距离都大于1的概率是：
P=1-
．
故答案为：1-
．
满足条件的正三角形ABC如下图所示：其中正三角形ABC的面积S三角形=
| ||
| 4 |
| 3 |
满足到正三角形ABC的顶点A、B、C的距离至少有一个小于1的平面区域如图中阴影部分所示，其加起来是一个半径为1的半圆，
则S阴影=
| 1 |
| 2 |
则使取到的点到三个顶点A、B、C的距离都大于1的概率是：
P=1-
| ||
| 6 |
故答案为：1-
| ||
| 6 |
看了 在边长为2的正三角形ABC内...的网友还看了以下：
设A是数集,且满足条件：若P属于A,P不为1,则（1-P）分之1属于A,证明集合A中至少有三个不同 2020-04-05 …
已知二次函数..已知二次函数y=-1/2x^+(n+1/2)x+n+1,它的图像与x轴交于点A（x 2020-05-13 …
概率论 P(B|A)+P(非B|非A)=1 求证A B 相互独立P(A),P(B)均大于0小于1, 2020-05-16 …
已知p^2-p-1=0,1-q-q^2=0,且pq不等于1.则pq+1/q1-q-q^2=0因为q 2020-06-07 …
概率论E(X)=∑kp(p-1)^(k-1)为什么等于1/p,怎么推导的? 2020-06-11 …
正方行abcd中,ab等于4,e为cd上点且de等于1,P为AC上一点,求PE＋PD最小值 2020-06-30 …
设p(A)大于0证明p(B/A)大于等于1-P(¯B)/P(A) 2020-07-18 …
如图,等腰rt三角形aob在平面直角坐标系中,p为动点,且pa丄pa.(1)如图1,P在第一象限, 2020-07-20 …
在矩形ABCD中,AB=8,AD=10,P是射线DA上一点,将三角板的直角顶点置于点P,三角板的两 2020-07-30 …
(1/2)“直线y=1/2+2分别交x,y轴于点A,C.P点是该直线上在第一象限内的点,PB垂直x 2020-07-31 …