早教吧作业答案频道 -->数学-->
如图,AB是O的直径,点C、D在圆上,且四边形AOCD是平行四边形,过点D作O的切线,分别交OA延长线与OC延长线于点E、F,连接BF.(1)求证:BF是O的切线;(2)已知圆的半径为1,求EF的长.
题目详情
如图,AB是 O的直径,点C、D在圆上,且四边形AOCD是平行四边形,过点D作 O的切线,分别交OA延长线与OC延长线于点E、F,连接BF.
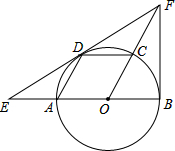
(1)求证:BF是 O的切线;
(2)已知圆的半径为1,求EF的长.

(1)求证:BF是 O的切线;
(2)已知圆的半径为1,求EF的长.
▼优质解答
答案和解析
(1)证明:连结OD,如图,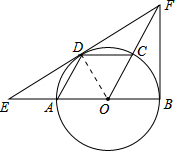 ∵四边形AOCD是平行四边形,
∵四边形AOCD是平行四边形,
而OA=OC,
∴四边形AOCD是菱形,
∴△OAD和△OCD都是等边三角形,
∴∠AOD=∠COD=60°,
∴∠FOB=60°,
∵EF为切线,
∴OD⊥EF,
∴∠FDO=90°,
在△FDO和△FBO中
,
∴△FDO≌△FBO,
∴∠ODF=∠OBF=90°,
∴OB⊥BF,
∴BF是 O的切线;
(2) 在Rt△OBF中,∵∠FOB=60°,
而tan∠FOB=
,
∴BF=1×tan60°=
.
∵∠E=30°,
∴EF=2BF=2
.
 ∵四边形AOCD是平行四边形,
∵四边形AOCD是平行四边形,而OA=OC,
∴四边形AOCD是菱形,
∴△OAD和△OCD都是等边三角形,
∴∠AOD=∠COD=60°,
∴∠FOB=60°,
∵EF为切线,
∴OD⊥EF,
∴∠FDO=90°,
在△FDO和△FBO中
|
∴△FDO≌△FBO,
∴∠ODF=∠OBF=90°,
∴OB⊥BF,
∴BF是 O的切线;
(2) 在Rt△OBF中,∵∠FOB=60°,
而tan∠FOB=
| BF |
| OB |
∴BF=1×tan60°=
| 3 |
∵∠E=30°,
∴EF=2BF=2
| 3 |
看了 如图,AB是O的直径,点C、...的网友还看了以下:
圆0和o'都经过点A,B.点P在BA延长线上,过P作圆O的割线PCD交圆0于CD两点作圆o'的切线P 2020-03-31 …
已知圆o:x^2y^2=4和点M(1,a).若a=3,求过点M作圆O的切线的切线长已知圆o:x^2 2020-04-27 …
(1)操作、观察:任意画⊙O,在⊙O内任取一点P(不为圆心),过点P直线l,交⊙O于点A、B.若直 2020-05-13 …
如图,PB切⊙O于B点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A 2020-05-17 …
如图,BD是直径,过圆O上一点A作圆O切线交DB延长线于P,过点B作BC平行PA交圆O于C,连接A 2020-06-06 …
自圆心O向圆外一直线MN作垂线OA,A为垂足.过A作圆的割线ABC及ADE,如果CD及EB的延长线 2020-07-31 …
(2014•聊城)如图,AB,AC分别是半⊙O的直径和弦,OD⊥AC于点D,过点A作半⊙O的切线AP 2020-11-13 …
如图,OA,OD是O半径,过A作O的切线,交∠AOD的平分线于点C,连接CD,延长AO交O于点E,交 2020-11-26 …
探究:在图中找出一组相等的线段(半径除外),并证明你的结论.OA,OB是圆O的半径,且OA垂直OB, 2020-12-05 …
如图,过圆O外一点P分别作圆O的切线PA和割线PBC,其中A为切点,过点A作PC的平行线交圆O于点D 2020-12-05 …