早教吧作业答案频道 -->数学-->
已知在直角坐标系中,抛物线y=ax2-8ax+3(a<0)与y轴交于点A,顶点为D,其对称轴交x轴于点B,点P在抛物线上,且位于抛物线对称轴的右侧.(1)当AB=BD时(如图),求抛物线的表达式;(2
题目详情
已知在直角坐标系中,抛物线y=ax2-8ax+3(a<0)与y轴交于点A,顶点为D,其对称轴交x轴于点B,点P在抛物线上,且位于抛物线对称轴的右侧.
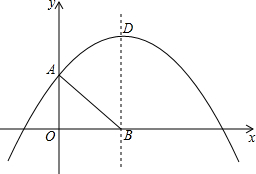
(1)当AB=BD时(如图),求抛物线的表达式;
(2)在第(1)小题的条件下,当DP∥AB时,求点P的坐标;
(3)点G在对称轴BD上,且∠AGB=
∠ABD,求△ABG的面积.

(1)当AB=BD时(如图),求抛物线的表达式;
(2)在第(1)小题的条件下,当DP∥AB时,求点P的坐标;
(3)点G在对称轴BD上,且∠AGB=
| 1 |
| 2 |
▼优质解答
答案和解析
(1)∵y=ax2-8ax+3=a(x-4)2+3-16a,
∴对称轴为x=4,B(4,0),A(0,3),
∴AB=5,
∵AB=BD,
∴BD=5,
∵抛物线的顶点为D,其对称轴交x轴于点B,
∴3-16a=BD=5,
∴a=-
,
∴y=
x2+x+3,
(2)∵B(4,0),A(0,3),
∴直线AB解析式为y=-
x+3,
∵DP∥AB,
设直线DP解析式为y=-
x+b,
∵D(4,5)在直线DP上,
∴b=8,
∴直线DP解析式为y=-
x+8,
由
,
∴x1=10,x2=4(舍),
∴P(10,
);
(3)如图
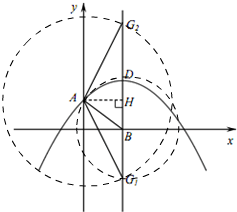
①以B为圆心,BA为半径作圆,交DB延长线于G1,
∵BG=AB,
∴∠BAG1=∠BG1A,
∴∠AGB=
∠ABD,
∵AB=5,点G在对称轴BD上x=4,
∴G1(4,-5),
∴S△ABG1=
×BG1×AH=
×5×4=10;
②以A为圆心,AG1为半径作圆,交BD延长线于G2,
过点A作AH⊥BD于H,
∴HG2=HG1=BH+BG1=8,
∴BG2=11,
∴G2(4,11),
S△ABG2=
×BG2×AH=
×11×4=22;
即:S△ABG=10或22,
∴对称轴为x=4,B(4,0),A(0,3),
∴AB=5,
∵AB=BD,
∴BD=5,
∵抛物线的顶点为D,其对称轴交x轴于点B,
∴3-16a=BD=5,
∴a=-
| 1 |
| 8 |
∴y=
| 1 |
| 8 |
(2)∵B(4,0),A(0,3),
∴直线AB解析式为y=-
| 3 |
| 4 |
∵DP∥AB,
设直线DP解析式为y=-
| 3 |
| 4 |
∵D(4,5)在直线DP上,
∴b=8,
∴直线DP解析式为y=-
| 3 |
| 4 |
由
|
∴x1=10,x2=4(舍),
∴P(10,
| 1 |
| 2 |
(3)如图

①以B为圆心,BA为半径作圆,交DB延长线于G1,
∵BG=AB,
∴∠BAG1=∠BG1A,
∴∠AGB=
| 1 |
| 2 |
∵AB=5,点G在对称轴BD上x=4,
∴G1(4,-5),
∴S△ABG1=
| 1 |
| 2 |
| 1 |
| 2 |
②以A为圆心,AG1为半径作圆,交BD延长线于G2,
过点A作AH⊥BD于H,
∴HG2=HG1=BH+BG1=8,
∴BG2=11,
∴G2(4,11),
S△ABG2=
| 1 |
| 2 |
| 1 |
| 2 |
即:S△ABG=10或22,
看了 已知在直角坐标系中,抛物线y...的网友还看了以下:
在平面直角坐标系中,已知抛物线y=-x的平方+bx+c与x轴交于点A、B(点A在点B的左侧),与y 2020-05-16 …
已知二次函数y=x^2-(m^2+8)x+2(m^2+6),设抛物线顶点为A,与X轴交于B,C两点 2020-05-16 …
在平面直角坐标系中,已知抛物线y=-x^2+bx+c与x轴交于点AB(点 A在点 B的左侧),与 2020-05-16 …
平面直角坐标系中,已知抛物线y=-x2+bx+c与x轴交于点A,B点A在点B的左侧,与y轴的正半轴 2020-05-16 …
已知抛物线y=1/2平方-x+k与x轴有两个交点(1)求k取值范围(2)设抛物线与x轴交于A.B2 2020-06-14 …
已知抛物线y=x2-4x-121)求抛物线与x轴交点A,B的坐标2)若抛物线顶点为P,求三角形PA 2020-06-14 …
当抛物线y=ax2+bx+c与x轴两交点及抛物线上一点P组成以P为直角顶点的直角三角形时,则点P的 2020-07-21 …
如图,抛物线y=ax2+bx-3与x轴交于A(-1,0)、B两点,与y轴交于点C,S△ABC=6.( 2020-11-01 …
如图,已知抛物线y=ax2-2ax+b与x轴交于A、B(3,0)两点,与y轴交于C,且OC=3OA, 2021-01-10 …
(2011.浙江)如图,在直角坐标系中,抛物线y=ax^2+bx+c与x轴交与点A(﹣1,0)如图, 2021-01-10 …