早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠BAC为钝角,边AB、AC的垂直平分线分别交BC于点D、E.(1)若BD2+CE2=DE2,则∠BAC的度数;(2)若∠ABC的平分线BF和边AC的垂直平分线EF相交于点F,过点F作FG垂直于BA的延长线
题目详情
如图,在△ABC中,∠BAC为钝角,边AB、AC的垂直平分线分别交BC于点D、E.
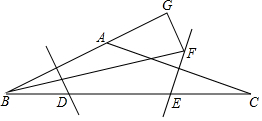
(1)若BD2+CE2=DE2,则∠BAC的度数;
(2)若∠ABC的平分线BF和边AC的垂直平分线EF相交于点F,过点F作FG垂直于BA的延长线于点G.求证:BC-AB=2AG.

(1)若BD2+CE2=DE2,则∠BAC的度数;
(2)若∠ABC的平分线BF和边AC的垂直平分线EF相交于点F,过点F作FG垂直于BA的延长线于点G.求证:BC-AB=2AG.
▼优质解答
答案和解析
(1)如图1中,连接AD、AE.
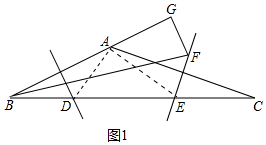
∵边AB、AC的垂直平分线分别交BC于点D、E,
∴BD=DA,EA=EC,
∴∠DBA=∠DAB,∠EAC=∠C,设∠DBA=∠DAB=x,∠EAC=∠C=y,
∵BD2+CE2=DE2,
∴AD2+AE2=DE2,
∴∠DAE=90°,
∴2x+90°+2y=180°,
∴x+y=45°,
∴∠BAC=x+y+90°=135°.
(2)证明:如图2中,连接AF,FC,作FM⊥CB于M,
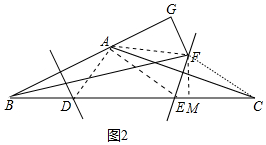
∵BF平分∠CBA,FG⊥BA,FM⊥CB,
∴FG=FM(角平分线上的点到角的两边距离相等),
在Rt△BFG和Rt△BFM中,
∴Rt△BFG≌Rt△CFM,
∴BG=BM,
∵EF垂直平分线AC,
∴FA=FC(垂直平分线上的点到线段两端点距离相等),
∵FG=FM,∠AFD=∠DMB=90°,
在Rt△AFG和Rt△CFM中,
,
∴Rt△AFG≌Rt△CFM,
∴CM=AG,
∵BC=BM+CM,BG=AB+AG,BG=BM,CM=AG,
∴BC=AB+2AG,
∴BC-AB=2AG.

∵边AB、AC的垂直平分线分别交BC于点D、E,
∴BD=DA,EA=EC,
∴∠DBA=∠DAB,∠EAC=∠C,设∠DBA=∠DAB=x,∠EAC=∠C=y,
∵BD2+CE2=DE2,
∴AD2+AE2=DE2,
∴∠DAE=90°,
∴2x+90°+2y=180°,
∴x+y=45°,
∴∠BAC=x+y+90°=135°.
(2)证明:如图2中,连接AF,FC,作FM⊥CB于M,

∵BF平分∠CBA,FG⊥BA,FM⊥CB,
∴FG=FM(角平分线上的点到角的两边距离相等),
在Rt△BFG和Rt△BFM中,
|
∴Rt△BFG≌Rt△CFM,
∴BG=BM,
∵EF垂直平分线AC,
∴FA=FC(垂直平分线上的点到线段两端点距离相等),
∵FG=FM,∠AFD=∠DMB=90°,
在Rt△AFG和Rt△CFM中,
|
∴Rt△AFG≌Rt△CFM,
∴CM=AG,
∵BC=BM+CM,BG=AB+AG,BG=BM,CM=AG,
∴BC=AB+2AG,
∴BC-AB=2AG.
看了 如图,在△ABC中,∠BAC...的网友还看了以下:
若AB向量=DC向量,则四边形ABCD是平行四边形.这是否是真命题?同时求它的逆否命题,在我们20 2020-05-16 …
小英沿边线从A经过B.C到D,走了4.2米,小兰沿边线从A经过D.C到B,走了4.8米,长方形AB 2020-05-24 …
1.若角a与角β的终边互为反向延长线则a与β的关系——?2.设A1=7.412,A2=-9.99, 2020-06-07 …
判断题1.向量a与向量b平行,则a与b的方向相同或相反.(错)为什么?2向量AB与向量CD共线,则 2020-08-01 …
零向量与任意非零向量共线是正确的,任意非零向量与零向量共线是错的,为什么?“向量a、b共线,b、c 2020-08-01 …
高数问题,快来啊~~设向量a,b,c均为非零向量,证明下面结论:1.若三个向量中任意两个不共线,但 2020-08-01 …
1.在平行四边形ABCD中,AC为一条对角线,若向量AB=(2,4),向量AC=(1,3),则向量 2020-08-02 …
1.下面说法正确的是A.若直线a平行于平面a(阿尔法)内的无数条直线,则a平行于a(阿尔法)B.若直 2020-11-06 …
高一向量1、若AB=DC,则依次连接A、B、C、D可得到一个平行四边形2、若a平行于b,b平行于c, 2020-12-07 …
如果角a与角b的终边互为反向延长线,则a与b的关系是什么 2021-01-15 …