早教吧作业答案频道 -->数学-->
如图,经过原点的抛物线y=-x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B,记点B关于抛物线对称轴的对称点为C(点B,点C不重合).连接CB,CP.(
题目详情
如图,经过原点的抛物线y=-x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B,记点B关于抛物线对称轴的对称点为C(点B,点C不重合).连接CB,CP.
(1)当m=3时,求点A的坐标及BC的长;
(2)当m>1时,连接CA,问m为何值时CA⊥CP?
(3)当m>1时过点P作PE⊥PC且PE=PC,问是否存在m,使得点E落在坐标轴上?若存在,求出所有满足要求的m的值,并定出相对应的点E坐标;若不存在,请说明理由.

(1)当m=3时,求点A的坐标及BC的长;
(2)当m>1时,连接CA,问m为何值时CA⊥CP?
(3)当m>1时过点P作PE⊥PC且PE=PC,问是否存在m,使得点E落在坐标轴上?若存在,求出所有满足要求的m的值,并定出相对应的点E坐标;若不存在,请说明理由.
▼优质解答
答案和解析
(1)当m=3时,y=-x2+6x=-x(x-6).
令y=0得:-x(x-6)=0,解得x=0或x=6,
∴点A的坐标为(6,0).
∴抛物线的对称轴为直线x=3.
∵B、C关于直线x=3对称,
∴BC=2×(3-1)=4.
(2)如图1所示:过点C作AH⊥x轴,垂足为H.
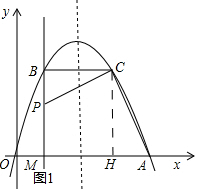
∵抛物线y=-x2+2mx的对称轴为x=m,
∴点B和点C直线x=m对称.
∵当x=1时,y=2m-1,
∴点B的坐标为(1,2m-1).
∴PB=m-1.
∵点B与点C关于直线x=m对称,
∴C(2m-1,2m-1).
∴BC=2m-2.
∴H(2m-1,0).
∴AH=1,CH=2m-1.
∵∠ACH=∠PCB=90°,
∴∠ACH=∠BCP.
又∵∠AHC=∠PCB=90°,
∴△ACH∽△PCB.
∴
=
,即
=
,
∴m=
.
(3)当m>1时,BC=2(m-1),PM=m,BP=m-1.
①若点E在x轴上时,如图2所示:
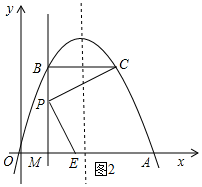
∵∠CPE=90°,
∴∠MPE+∠BPC=∠MPE+∠MEP=90°,
∴∠BPC=∠MEP.
在△BPC和△MEP中,
,
∴△BPC≌△MEP.
∴BC=PM.
∴2(m-1)=m,解得m=2,
∴E(2,0).
若点E在y轴上,如图3所示:过点P作PN⊥y轴与点N.
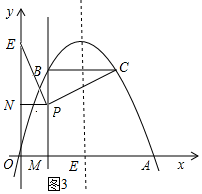
∵∠EPC=90°,
∴∠EPB+∠BPC=90°.
∵∠NPE+∠EPB=90°,∠NEP=∠EPB,
∴∠BPC=∠EPN.
在△EPN和△CPB中,
∴△BPC≌△NPE.
∴BP=NP=OM=1,
∴m-1=1,
∴m=2
∴E(0,4).
综上所述,当m=2时,点E的坐标为(2,0)或(0,4).
令y=0得:-x(x-6)=0,解得x=0或x=6,
∴点A的坐标为(6,0).
∴抛物线的对称轴为直线x=3.
∵B、C关于直线x=3对称,
∴BC=2×(3-1)=4.
(2)如图1所示:过点C作AH⊥x轴,垂足为H.

∵抛物线y=-x2+2mx的对称轴为x=m,
∴点B和点C直线x=m对称.
∵当x=1时,y=2m-1,
∴点B的坐标为(1,2m-1).
∴PB=m-1.
∵点B与点C关于直线x=m对称,
∴C(2m-1,2m-1).
∴BC=2m-2.
∴H(2m-1,0).
∴AH=1,CH=2m-1.
∵∠ACH=∠PCB=90°,
∴∠ACH=∠BCP.
又∵∠AHC=∠PCB=90°,
∴△ACH∽△PCB.
∴
| AH |
| CH |
| PB |
| BC |
| 1 |
| 2m-1 |
| m-1 |
| 2(m-1) |
∴m=
| 3 |
| 2 |
(3)当m>1时,BC=2(m-1),PM=m,BP=m-1.
①若点E在x轴上时,如图2所示:

∵∠CPE=90°,
∴∠MPE+∠BPC=∠MPE+∠MEP=90°,
∴∠BPC=∠MEP.
在△BPC和△MEP中,
|
∴△BPC≌△MEP.
∴BC=PM.
∴2(m-1)=m,解得m=2,
∴E(2,0).
若点E在y轴上,如图3所示:过点P作PN⊥y轴与点N.

∵∠EPC=90°,
∴∠EPB+∠BPC=90°.
∵∠NPE+∠EPB=90°,∠NEP=∠EPB,
∴∠BPC=∠EPN.
在△EPN和△CPB中,
|
∴△BPC≌△NPE.
∴BP=NP=OM=1,
∴m-1=1,
∴m=2
∴E(0,4).
综上所述,当m=2时,点E的坐标为(2,0)或(0,4).
看了 如图,经过原点的抛物线y=-...的网友还看了以下:
反比例函数的图像与双曲线的图像很相像,并且其图像的x,y轴又与双曲线的渐近线又有异曲同工之妙.请问 2020-04-08 …
如图,抛物线y=a(x+1)(x-5)与x轴的交点为M、N.直线y=kx+b 与x轴交于P(-2, 2020-05-13 …
二次函数y=1-6x-3x2的顶点坐标和对称轴方程分别是[]A.顶点(1,4),对称轴x=1B.顶 2020-05-13 …
二次函数Y=(2/3)x^2图象在x轴上方,顶点坐标(0,0 )为原点A0,点A1,A2,A3,… 2020-05-16 …
已知抛物线Y等于aX²—2X+c与它的对称轴相较于点A(1,-4),与y轴交与点C,与X轴正半轴交 2020-05-16 …
已知抛物线y=ax^2-2x+c与它的对称轴相交与点A(1,-4),与y轴交于点C,与x轴正半轴交 2020-05-16 …
抛物线C的焦点轴x正半轴上且顶点在原点 抛物线C上一点(m,2)到焦点的距离是5/2,则抛物线C的 2020-05-16 …
已知二次函数y=ax2+bx+c的图像与x轴交于A、B两点,与y轴交于点C,其中点B在x轴的正已知 2020-05-16 …
已知二次函数 y=x²-(m²+8)x+2(m²+6).(1)求证:不论m取任何实数,此函数图像都 2020-05-16 …
如图:已知抛物线与X轴交于A、B两点,与Y轴正半轴交于C点,直线X=1是抛物线的对称轴,如图:已知 2020-06-03 …