早教吧作业答案频道 -->数学-->
如图,四边形OABC是边长为2的正方形,点P为OA边上任意一点(与点O,A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥OA,交BO于点N,连接ND,BM,设OP=t.(1)求点M的坐标(
题目详情
如图,四边形OABC是边长为2的正方形,点P为OA边上任意一点(与点O,A不重合),连接CP,过点P作PM⊥CP交AB于点D,且PM=CP,过点M作MN∥OA,交BO于点N,连接ND,BM,设OP=t.
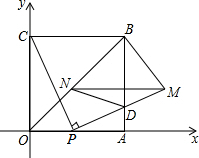
(1)求点M的坐标(用含t的代数式表示)
(2)试判断线段MN的长度是否随点P的位置的变化而改变?请说明理由.当t为何值时,四边形BNDM的面积最小.
(3)在(2)的结论下,若有一条以直线AB为对称轴,过C,M两点的抛物线,请思考,是否存在直线AB上一动点E,抛物线上一动点F,使得以点P,M,E,F为顶点的四边形是平行四边形?若存在,请直接写出满足要求的点F的坐标;若不存在,请说明理由.

(1)求点M的坐标(用含t的代数式表示)
(2)试判断线段MN的长度是否随点P的位置的变化而改变?请说明理由.当t为何值时,四边形BNDM的面积最小.
(3)在(2)的结论下,若有一条以直线AB为对称轴,过C,M两点的抛物线,请思考,是否存在直线AB上一动点E,抛物线上一动点F,使得以点P,M,E,F为顶点的四边形是平行四边形?若存在,请直接写出满足要求的点F的坐标;若不存在,请说明理由.
▼优质解答
答案和解析
(1)如图1中,过M作MG⊥OA于G,
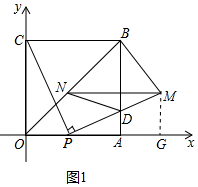
∵CP⊥PM,
∴∠CPO+∠MPG=90°,
又∵CO⊥OA,
∴∠CPO+∠OCP=90°,
∴∠MPG=∠OCP,
在△OCP和△GPM中,
,
∴△OCP≌△GPM,
∴MG=OP=t,PG=OC=2
∴M(2+t,t).
(2)∵四边形OABC是边长为2的正方形,
∴B(2,2),
∴直线OB的解析式为y=x,
又∵MN∥AO,
∴N(t,t),
∴MN=2,
∴MN的长度不随P的位置的变化而改变,
∵AB∥MG
∴△PAD∽△PMG,
∴
=
,
∴
=
,
∴AD=
,
∴BD=
,
∵BA⊥MN,
∴s=
•BD•MN=
•
•2=
(t-1)2+
,
∵
<0,
∴当t=1时,四边形BNDM的面积最小.
(3)如图2中,
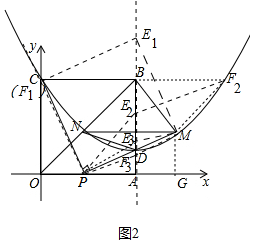
由图象可知当点F的横坐标为0或4或2,
∴点F的坐标为(0,2)或(4,2)或(2,
).

∵CP⊥PM,
∴∠CPO+∠MPG=90°,
又∵CO⊥OA,
∴∠CPO+∠OCP=90°,
∴∠MPG=∠OCP,
在△OCP和△GPM中,
|
∴△OCP≌△GPM,
∴MG=OP=t,PG=OC=2
∴M(2+t,t).
(2)∵四边形OABC是边长为2的正方形,
∴B(2,2),
∴直线OB的解析式为y=x,
又∵MN∥AO,
∴N(t,t),
∴MN=2,
∴MN的长度不随P的位置的变化而改变,
∵AB∥MG
∴△PAD∽△PMG,
∴
| PA |
| PG |
| PD |
| PM |
∴
| 2-t |
| 2 |
| AD |
| t |
∴AD=
| -t2+2t |
| 2 |
∴BD=
| t2-2t+4 |
| 2 |
∵BA⊥MN,
∴s=
| 1 |
| 2 |
| 1 |
| 2 |
| t2-2t+4 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∵
| 1 |
| 2 |
∴当t=1时,四边形BNDM的面积最小.
(3)如图2中,

由图象可知当点F的横坐标为0或4或2,
∴点F的坐标为(0,2)或(4,2)或(2,
| 2 |
| 3 |
看了 如图,四边形OABC是边长为...的网友还看了以下:
如图,在△ABC中,BE=EC,过点E作EG//BA叫AC于点G,过点A作AD//BC,与EG的延 2020-04-26 …
(安徽省濉溪县2009届高三第四次月考25题)一个生活在20世纪20年代初、家境较殷实的英国人可能 2020-05-14 …
已知:如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于已 2020-05-16 …
已知:如图,四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于点 2020-05-16 …
如图所示,在三角形ABC中,角BAC=90度,AB=AC,角ACB的平分线交AB于D,过B作CD的 2020-05-16 …
英文翻译DearMrxx感谢你对我工作的支持,经过仔细思考,我决定申请辞职。周二之前跟AMY完成我 2020-05-17 …
在团体人寿保险中,投保团体的被保险人员必须是能够参加正常工作的( )A.长期因病全休人员B.长期 2020-05-22 …
在团体人寿保险中,投保团体的被保险人员必须是能够参加正常工作的( )A.长期因病全休人员###SXB 2020-05-22 …
[HELP..]太阳能热水器已走进千家万户,有一容量为240升的太阳能热水器,设其工作时间为Y(分 2020-05-22 …
以无碎片直通方式工作的交换机对于以太网的帧中,哪部分内容不去读它(60)。A.原地址B.目的地址C. 2020-05-26 …