早教吧作业答案频道 -->数学-->
如图,抛物线y=-12x2+bx+3,与x轴交于点B(-2,0)和C,与y轴交于点A,点M在y轴上.(1)求抛物线的解析式;(2)连结BM并延长,交抛物线于D,过点D作DE⊥x轴于E.当以B、D、E为顶点的三角形
题目详情
如图,抛物线y=-
x2+bx+3,与x轴交于点B(-2,0)和C,与y轴交于点A,点M在y轴上.
(1)求抛物线的解析式;
(2)连结BM并延长,交抛物线于D,过点D作DE⊥x轴于E.当以B、D、E为顶点的三角形与△AOC相似时,求点M的坐标;
(3)连结BM,当∠OMB+∠OAB=∠ACO时,求AM的长.
| 1 |
| 2 |
(1)求抛物线的解析式;
(2)连结BM并延长,交抛物线于D,过点D作DE⊥x轴于E.当以B、D、E为顶点的三角形与△AOC相似时,求点M的坐标;
(3)连结BM,当∠OMB+∠OAB=∠ACO时,求AM的长.

▼优质解答
答案和解析
(1)将点B(-2,0)代入抛物线的解析式y=-
x2+bx+3得
-
×(-2)2-2b+3=0,
∴b=
,
∴抛物线的解析式为y=-
x2+
x+3.
(2)如图1中,
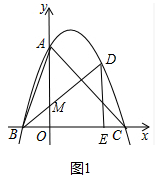
∵抛物线的解析式为y=-
x2+
x+3,与x轴交于B(-2,0),A(3,0),C(0,3),
∴OA=OC,
∴△AOC是等腰直角三角形,
∵OM∥DE,
∴△BMO∽△BDE,
∵要使B、D、E为顶点的三角形与△AOC相似,
∴只要△BOM∽△AOC,设M(0,m),
∴
=
,
∴
=
,
∴m=±2,
∴点M的坐标为(2,0)或(-2,0).
(3)如图2中,作AG⊥AC交x轴于G,BF⊥AG于F.
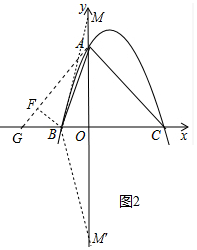
∵OA=OC,∠AOC=∠GAC=90°,
∴∠OAC=∠ACO=∠OAG=45°,
∵∠OMB+∠OAB=∠ACO=45°,
∴∠FAB=∠OMB,设M(n,0),
∵∠AFB=∠BOM=90°,
∴△AFB∽△MOB,
∴
=
,∵FB=
,AF=
,OB=2,
∴
=
,
∴n=±10,
∴点M的坐标为(0,10)或(0,-10).
| 1 |
| 2 |
-
| 1 |
| 2 |
∴b=
| 1 |
| 2 |
∴抛物线的解析式为y=-
| 1 |
| 2 |
| 1 |
| 2 |
(2)如图1中,

∵抛物线的解析式为y=-
| 1 |
| 2 |
| 1 |
| 2 |
∴OA=OC,
∴△AOC是等腰直角三角形,
∵OM∥DE,
∴△BMO∽△BDE,
∵要使B、D、E为顶点的三角形与△AOC相似,
∴只要△BOM∽△AOC,设M(0,m),
∴
| OM |
| OB |
| OA |
| OC |
∴
| |m| |
| 2 |
| 3 |
| 3 |
∴m=±2,
∴点M的坐标为(2,0)或(-2,0).
(3)如图2中,作AG⊥AC交x轴于G,BF⊥AG于F.

∵OA=OC,∠AOC=∠GAC=90°,
∴∠OAC=∠ACO=∠OAG=45°,
∵∠OMB+∠OAB=∠ACO=45°,
∴∠FAB=∠OMB,设M(n,0),
∵∠AFB=∠BOM=90°,
∴△AFB∽△MOB,
∴
| OM |
| AF |
| OB |
| FB |
| ||
| 2 |
5
| ||
| 2 |
∴
| |n| | ||||
|
| 2 | ||||
|
∴n=±10,
∴点M的坐标为(0,10)或(0,-10).
看了 如图,抛物线y=-12x2+...的网友还看了以下:
(2011•香坊区模拟)如图,在平面直角坐标系中,点.是坐标原点,AB∥y轴,将△ABO沿A0翻折 2020-05-24 …
真空中有一个电荷量为+Q的点电荷,固定在A点.在与A点相距为r的B点,电场强度大小为kQr2kQr 2020-06-12 …
如图,在菱形ABCD中,∠A=60°,AD=8,F是AB的中点.过点F作FE⊥AD,垂足为E.将△ 2020-06-15 …
在计算极值.拐点.最值是否都应考虑导数不存在点.如果原函数在导数不存在点有对应值.这样不存在的点为 2020-06-30 …
如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一 2020-07-14 …
与双曲线-y2=1有公共焦点,且离心率为.A,B分别是椭圆C的左顶点和右顶点.点S是椭圆C上位于x 2020-07-21 …
探究:如图.已知矩形0ABC,顶点A、C分别在x、y轴的正半轴上,点B的坐标为(8,4),M是BC 2020-07-22 …
如图,直线y=-34x+3与x轴,y轴交于A,B两点.点P是线段OB上的一动点(能与点O,B重合) 2020-07-24 …
如图所示,OO'为凸透镜的主光轴,将点光源放在A点时,像在B点;将点光源放在B点时,像在C点.当将 2020-07-29 …
如图,点M是矩形ABCD的边AD的中点.点P是BC边上一动点,PE⊥MC,PF⊥BM.垂足为E、F 2020-08-03 …