体积为183的正三棱锥A-BCD的每个顶点都在半径为R的球O的球面上，球心O在此三棱锥内部，且R：BC=2：3，点E为线段BD上一点，且DE=2EB，过点E作球O的截面，则所得截面圆面积的取值范围是（

Question

体积为18

√(3)的正三棱锥A-BCD的每个顶点都在半径为R的球O的球面上，球心O在此三棱锥内部，且R：BC=2：3，点E为线段BD上一点，且DE=2EB，过点E作球O的截面，则所得截面圆面积的取值范围是（　　）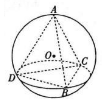

A. [4π，12π]

B. [8π，16π]

C. [8π，12π]

D. [12π，16π]

Answer 1

设BC=3a，则R=2a，
∵体积为18√(3)的正三棱锥A-BCD的每个顶点都在半径为R的球O的球面上，
∴(1)/(3)×(√(3))/(4)×9a2h=18√(3)，∴h=(24)/(a2)，
∵R²=（h-R）²+（√(3)a）²，∴4a²=（(24)/(a2)-2a）²+3a²，∴a=2，
∴BC=6，R=4，
∵点E为线段BD上一点，且DE=2EB，
∴△ODB中，OD=OB=4，DB=6，cos∠ODB=(3)/(4)，
∴OE=√(16+16-2×4×4×(3)/(4))=2√(2)，
截面垂直于OE时，截面圆的半径为√(16-8)=2√(2)，截面圆面积为8π，
以OE所在直线为直径时，截面圆的半径为4，截面圆面积为16π，
∴所得截面圆面积的取值范围是[8π，16π]．
故选：B．