早教吧作业答案频道 -->数学-->
已知三棱柱ABC-A1B1C1的侧棱和底面垂直,底面是正三角形,侧棱长是底边长的2倍,若该三棱柱的各顶点都在球O的表面上,且球O的表面积为36π,则此三棱锥A-A1B1C1的体积为()A.12125B.811
题目详情
已知三棱柱ABC-A1B1C1的侧棱和底面垂直,底面是正三角形,侧棱长是底边长的2倍,若该三棱柱的各顶点都在球O的表面上,且球O的表面积为36π,则此三棱锥A-A1B1C1的体积为( )
A. 121 25
B. 81 16
C. 16 9
D. 9 4
▼优质解答
答案和解析
如图,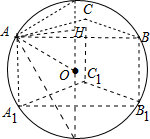
∵三棱柱ABC-A1B1C1的所有棱长都相等,6个顶点都在球O的球面上,
∴三棱柱为正三棱柱,且其中心为球的球心,设为O,
再设球的半径为r,由球O的表面积为36π,得4πr2=36π,∴r=3.
设三棱柱的底面边长为a,则上底面所在圆的半径为
a,且球心O到上底面中心H的距离OH=a,
∴32=a2+(
a)2,∴a=
.
则三棱柱的底面积为S=
×(
)2=
.
∴三棱锥A-A1B1C1的体积为
×
×2×
=
.
故选:B.

∵三棱柱ABC-A1B1C1的所有棱长都相等,6个顶点都在球O的球面上,
∴三棱柱为正三棱柱,且其中心为球的球心,设为O,
再设球的半径为r,由球O的表面积为36π,得4πr2=36π,∴r=3.
设三棱柱的底面边长为a,则上底面所在圆的半径为
| ||
| 3 |
∴32=a2+(
| ||
| 3 |
3
| ||
| 2 |
则三棱柱的底面积为S=
| ||
| 4 |
3
| ||
| 2 |
27
| ||
| 16 |
∴三棱锥A-A1B1C1的体积为
| 1 |
| 3 |
27
| ||
| 16 |
3
| ||
| 2 |
| 81 |
| 16 |
故选:B.
看了 已知三棱柱ABC-A1B1C...的网友还看了以下:
有两个侧面垂直于底面的四棱柱是直四棱柱吗?正三棱锥于正 2020-04-08 …
填空题:按是不是2的倍数可以把整数分成{}和{}两类,按因数的多少把非零自然数分成{}、{}和{} 2020-04-09 …
若正三棱锥的斜高是棱锥高的倍,则正棱锥的侧面积是底面积的()A.倍B.2倍C.倍D.3倍 2020-04-24 …
正方体的棱长大两倍,它的表面积就扩大()倍体积就扩大()倍棱长总和扩大()倍 2020-05-15 …
在一个二面角的一个面内有一点,它到棱的距离等于到另一个面的距离的2倍在二面角的一个面内有一点,它到 2020-05-16 …
一个正方体棱长扩大3倍.棱长总和扩大几倍?表面积扩大几倍?不用方程 2020-05-17 …
如图,在侧棱锥垂直于底面的三棱柱ABC-A1B1C1中,AC=3,AB=5,BC=4,AA1=4, 2020-06-04 …
若三棱锥A—ABC的底面是正三角形,且三条棱都相等,三棱锥的侧面积是底面积的2倍,棱锥高SO=3求 2020-06-04 …
《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,将底面为矩形,一条侧棱垂直于底面的四棱 2020-06-13 …
关于三棱锥和球的一道题(在线等!)有一侧棱都相等的三棱锥侧棱为2倍的根号2它内接于球内,球心距三棱 2020-06-21 …