早教吧作业答案频道 -->数学-->
如图,在Rt△ABC中,∠C=90°,以BC为直径的O交斜边AB于点M,若H是AC的中点,连接MH.(1)求证:MH为O的切线.(2)若MH=32,tan∠ABC=34,求O的半径.(3)在(2)的条件下分别过点A、B作O的
题目详情
如图,在Rt△ABC中,∠C=90°,以BC为直径的 O交斜边AB于点M,若H是AC的中点,连接MH.
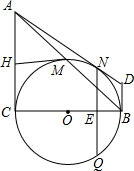
(1)求证:MH为 O的切线.
(2)若MH=
,tan∠ABC=
,求 O的半径.
(3)在(2)的条件下分别过点A、B作 O的切线,两切线交于点D,AD与 O相切于N点,过N点作NQ⊥BC,垂足为E,且交 O于Q点,求线段NQ的长度.

(1)求证:MH为 O的切线.
(2)若MH=
| 3 |
| 2 |
| 3 |
| 4 |
(3)在(2)的条件下分别过点A、B作 O的切线,两切线交于点D,AD与 O相切于N点,过N点作NQ⊥BC,垂足为E,且交 O于Q点,求线段NQ的长度.
▼优质解答
答案和解析
(1)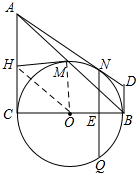 连接OH、OM,
连接OH、OM,
∵H是AC的中点,O是BC的中点,
∴OH是△ABC的中位线,
∴OH∥AB,
∴∠COH=∠ABC,∠MOH=∠OMB,
又∵OB=OM,
∴∠OMB=∠MBO,
∴∠COH=∠MOH,
在△COH与△MOH中,
,
∴△COH≌△MOH(SAS),
∴∠HCO=∠HMO=90°,
∴MH是 O的切线;
(2)∵MH、AC是 O的切线,
∴HC=MH=
,
∴AC=2HC=3,
∵tan∠ABC=
,
∴
=
,
∴BC=4,
∴ O的半径为2;
(3)连接OA、CN、ON,OA与CN相交于点I,
∵AC与AN都是 O的切线,
∴AC=AN,AO平分∠CAD,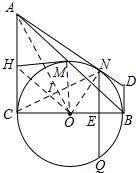
∴AO⊥CN,
∵AC=3,OC=2,
∴由勾股定理可求得:AO=
,
∵
AC•OC=
AO•CI,
∴CI=
,
∴由垂径定理可求得:CN=
,
设OE=x,
由勾股定理可得:CN2-CE2=ON2-OE2,
∴
-(2+x)2=4-x2,
∴x=
,
∴CE=
,
由勾股定理可求得:EN=
,
∴由垂径定理可知:NQ=2EN=
.
 连接OH、OM,
连接OH、OM,∵H是AC的中点,O是BC的中点,
∴OH是△ABC的中位线,
∴OH∥AB,
∴∠COH=∠ABC,∠MOH=∠OMB,
又∵OB=OM,
∴∠OMB=∠MBO,
∴∠COH=∠MOH,
在△COH与△MOH中,
|
∴△COH≌△MOH(SAS),
∴∠HCO=∠HMO=90°,
∴MH是 O的切线;
(2)∵MH、AC是 O的切线,
∴HC=MH=
| 3 |
| 2 |
∴AC=2HC=3,
∵tan∠ABC=
| 3 |
| 4 |
∴
| AC |
| BC |
| 3 |
| 4 |
∴BC=4,
∴ O的半径为2;
(3)连接OA、CN、ON,OA与CN相交于点I,
∵AC与AN都是 O的切线,
∴AC=AN,AO平分∠CAD,

∴AO⊥CN,
∵AC=3,OC=2,
∴由勾股定理可求得:AO=
| 13 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴CI=
6
| ||
| 13 |
∴由垂径定理可求得:CN=
12
| ||
| 13 |
设OE=x,
由勾股定理可得:CN2-CE2=ON2-OE2,
∴
| 144 |
| 13 |
∴x=
| 10 |
| 13 |
∴CE=
| 10 |
| 13 |
由勾股定理可求得:EN=
| 24 |
| 13 |
∴由垂径定理可知:NQ=2EN=
| 48 |
| 13 |
看了 如图,在Rt△ABC中,∠C...的网友还看了以下:
PCR产物的酶切问题PCR产物进行taqI内切酶酶切鉴定 结果出现了几条杂带 分析原因可能为条带内 2020-05-16 …
f(x)=1/3x^3+bx^2+cx+d,h(x+1-t)>h(2x+2)已知函数f(x)=1/ 2020-06-03 …
切烧饼的秘密?若把一个大烧饼切10刀(不允许重复),则最多可以切多少块小饼?切N刀呢?(提示:因为 2020-06-15 …
小船在静水中速度为14.4km/h,河水速度为10.8km/h,河宽600m,求(1)若要小船以最 2020-06-17 …
如图,在Rt△ABC中,∠C=90°,以BC为直径的O交斜边AB于点M,若H是AC的中点,连接MH 2020-07-20 …
初二数学选择题在三角形ABC中,它底边为A,底边上的高为H,则三角形的面积S=1/2AH.若H为定 2020-07-31 …
(2012•乐山)如图,⊙O是四边形ABCD的内切圆,E、F、G、H是切点,点P是优弧EFH上异于 2020-07-31 …
已知函数f(x)=x2-(a+2)x+alnx.其中常数a>0(Ⅰ)讨论函数f(x)的单调性;(Ⅱ 2020-08-01 …
知道球体直径和切面高度,可以求出切面的直径吗已知球体直径R,在球面往球心的某高度h做切面,怎么求出切 2020-11-26 …
飞机的高度为H以v1速度飞行扔下一炸弹与飞机水平距离为s的地面拦截系统同时以v2速度竖直向上发射一炮 2021-01-06 …