早教吧作业答案频道 -->数学-->
如图1,已知△ABC中,AB=AC,点D是△ABC外的一点(与点A分别在直线BC的两侧),且DB=DC,过点D作DE∥AC,交射线AB于点E,连接AD交BC于点F.(1)求证:AD垂直平分BC;(2)请从A,B两题中任选一
题目详情
如图1,已知△ABC中,AB=AC,点D是△ABC外的一点(与点A分别在直线BC的两侧),且DB=DC,过点D作DE∥AC,交射线AB于点E,连接AD交BC于点F.
(1)求证:AD垂直平分BC;
(2)请从A,B两题中任选一题作答,我选择___题.
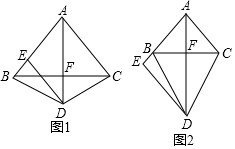
A:如图1,当点E在线段AB上且不与点B重合时,求证:DE=AE;
B:如图2,当点E在线段AB的延长线上时,写出线段DE,AC,BE之间的等量关系,并证明你的结论.
(1)求证:AD垂直平分BC;
(2)请从A,B两题中任选一题作答,我选择___题.
A:如图1,当点E在线段AB上且不与点B重合时,求证:DE=AE;
B:如图2,当点E在线段AB的延长线上时,写出线段DE,AC,BE之间的等量关系,并证明你的结论.

▼优质解答
答案和解析
(1)∵AB=AC,
∴点A在线段BC的垂直平分线上,
∵DB=DC,
∴点D在线段BC的垂直平分线上,
∴AD垂直平分BC;
(2)A、由(1)得,AD⊥BC,
∵AB=AC,
∴∠BAF=∠CAF,
∵DE∥AC,
∴∠CAF=∠ADE,
∴∠BAF=∠ADE,
∴DE=AE;
B、DE=BE+AC,
由(1)得AF⊥BC,
∵AB=AC,
∴∠BAF=∠CAE,
∵DE∥AC,
∴∠EDA=∠CAF,
∴∠BAF=∠EDA
∴EA=ED,
∵EA=EB+BA=EB+AC,
∴DE=BE+AC.
∴点A在线段BC的垂直平分线上,
∵DB=DC,
∴点D在线段BC的垂直平分线上,
∴AD垂直平分BC;
(2)A、由(1)得,AD⊥BC,
∵AB=AC,
∴∠BAF=∠CAF,
∵DE∥AC,
∴∠CAF=∠ADE,
∴∠BAF=∠ADE,
∴DE=AE;
B、DE=BE+AC,
由(1)得AF⊥BC,
∵AB=AC,
∴∠BAF=∠CAE,
∵DE∥AC,
∴∠EDA=∠CAF,
∴∠BAF=∠EDA
∴EA=ED,
∵EA=EB+BA=EB+AC,
∴DE=BE+AC.
看了 如图1,已知△ABC中,AB...的网友还看了以下:
设有一5阶上三角矩阵A[1..5,1..5],现将其上三角中的元素按列优先顺序存放在一堆数组B[1 2020-04-13 …
规定:a△b=a+(a+1)+(a+2)+···+(a+b-1),其中a、b表示自然数.1.求1△ 2020-05-20 …
将一个A[1..100,1..100]的三对角矩阵,按行优先存入一维数组B[1..298]中,A中元 2020-05-26 …
先分解因式,再求值:(1)(x+2)(x-3)(x-7)+(2+x)(3-x)(x+3),其中x= 2020-06-03 …
1.已知集合S={x|1<x≤7},A={x|2≤x<5},B={x|3≤x<7},求:1.(A在 2020-07-30 …
高手多元二次方程是否可解,(Am+Bn+Cp)x+(Ca+Db)y=Mx+y=1;m+n+p=1; 2020-08-02 …
整式综合1.求[8+2(k-1)][60-3(k-1)]的最小值.2.已知1/(a-b)+1/(b- 2020-10-31 …
1.已知自然数a,b,c,满足a^2+b^2+c^2+420,则代数式1/a+1/b+1/c的值为? 2020-10-31 …
关于秩和特征值的问题刘老师,您好!请问:我在一个题目的答案里看到这样的解释:1矩阵B=[1]*[1, 2020-11-11 …
下列叙述正确的是()A.1.00moLNacL中含有6.02x10^23个NacL分子B.1.00m 2021-02-05 …