早教吧作业答案频道 -->数学-->
如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC于点E,经过点A、D、E的圆的圆心F恰好在y轴上,⊙F与y轴相交于另一点G.(1)求证:BC是⊙F的切线
题目详情
如图,在平面直角坐标系中,Rt△ABC的斜边AB在y轴上,边AC与x轴交于点D,AE平分∠BAC交边BC于点E,经过点A、D、E的圆的圆心F恰好在y轴上,⊙F与y轴相交于另一点G.
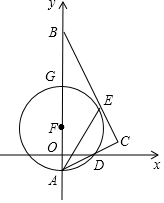
(1)求证:BC是⊙F的切线;
(2)若点A、D的坐标分别为A(0,-1),D(2,0),求⊙F的半径;
(3)试探究线段AG、AD、CD三者之间满足的等量关系,并证明你的结论.

(1)求证:BC是⊙F的切线;
(2)若点A、D的坐标分别为A(0,-1),D(2,0),求⊙F的半径;
(3)试探究线段AG、AD、CD三者之间满足的等量关系,并证明你的结论.
▼优质解答
答案和解析
(1)证明: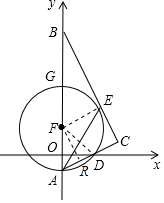 连接EF,
连接EF,
∵AE平分∠BAC,
∴∠FAE=∠CAE,
∵FA=FE,
∴∠FAE=∠FEA,
∴∠FEA=∠EAC,
∴FE∥AC,
∴∠FEB=∠C=90°,即BC是⊙F的切线;
(2) 连接FD,
设⊙F的半径为r,
则r2=(r-1)2+22,
解得,r=
,即⊙F的半径为
;
(3) AG=AD+2CD.
证明:作FR⊥AD于R,
则∠FRC=90°,又∠FEC=∠C=90°,
∴四边形RCEF是矩形,
∴EF=RC=RD+CD,
∵FR⊥AD,
∴AR=RD,
∴EF=RD+CD=
AD+CD,
∴AG=2FE=AD+2CD.
 连接EF,
连接EF,∵AE平分∠BAC,
∴∠FAE=∠CAE,
∵FA=FE,
∴∠FAE=∠FEA,
∴∠FEA=∠EAC,
∴FE∥AC,
∴∠FEB=∠C=90°,即BC是⊙F的切线;
(2) 连接FD,
设⊙F的半径为r,
则r2=(r-1)2+22,
解得,r=
| 5 |
| 2 |
| 5 |
| 2 |
(3) AG=AD+2CD.
证明:作FR⊥AD于R,
则∠FRC=90°,又∠FEC=∠C=90°,
∴四边形RCEF是矩形,
∴EF=RC=RD+CD,
∵FR⊥AD,
∴AR=RD,
∴EF=RD+CD=
| 1 |
| 2 |
∴AG=2FE=AD+2CD.
看了 如图,在平面直角坐标系中,R...的网友还看了以下:
1若a,b,x,y属于正数,证明:x分之a平方+y分之b平方大于等于(x+y)分之(a+b)的平方 2020-06-02 …
已知集合A={2-a小于等于x小于等于2+a},B={x小于等于1或x大于等于4},(1).当a= 2020-07-30 …
已知集合A={X|3≤X<8}B={4<X<6}(1)求B相对于R的补集∩A(2)已知C={X|a 2020-07-30 …
这种说法有道理么,全集U=A∪B则CuB=A上面是别人说的,我觉得这样不对比如U={1,2,3,4 2020-07-30 …
对于有理数ab./a十b/=/a/+/b/一定成立吗?如果一定成立,请说明理由.如果不一定成立对于 2020-07-31 …
计算:已知a分之1加b分之1=根号5(a不等于b)求b(a-b)分之a减a(a-b)分之计算:已知 2020-08-01 …
已知a、b都是正数,且a不等于b根号21.求证:根号2在a/b与(a+2b)/(a+b)之间2.a 2020-08-01 …
有限集合P中的个数记作card(P).一直card(M)=10,A包含于M,B包含于M,A∩B=空 2020-08-01 …
已知集合A={x|x2+ax-12=0},B={x|x2+bx+c=0},且A不等于B,A并B={ 2020-08-02 …
如果a大于b,则下列不等式成立的是A,ab大于0B,a-b大于0C,绝对值a大于绝对值b如果a大于 2020-08-03 …