早教吧作业答案频道 -->数学-->
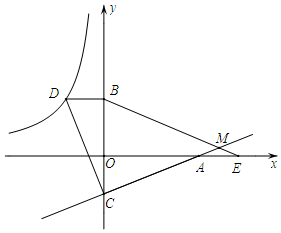
如图,已知点D在反比例函数y=mx的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=23.(1)求反比例函数y=mx和直线y=kx+b的解析式;(2
题目详情
如图,已知点D在反比例函数y=
的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=
.
(1)求反比例函数y=
和直线y=kx+b的解析式;
(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;
(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA与点M,求∠BMC的度数.
| m |
| x |
| 2 |
| 3 |

(1)求反比例函数y=
| m |
| x |
(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;
(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA与点M,求∠BMC的度数.
▼优质解答
答案和解析
(1)∵A(5,0),
∴OA=5.
∵tan∠OAC=
,
∴
=
,解得OC=2,
∴C(0,-2),
∴BD=OC=2,
∵B(0,3),BD∥x轴,
∴D(-2,3),
∴m=-2×3=-6,
∴y=
,
设直线AC关系式为y=kx+b,
∵过A(5,0),C(0,-2),
∴
,解得
,
∴y=
x-2;
(2)∵B(0,3),C(0,-2),
∴BC=5=OA,
在△OAC和△BCD中
∴△OAC≌△BCD(SAS),
∴AC=CD,
∴∠OAC=∠BCD,
∴∠BCD+∠BCA=∠OAC+∠BCA=90°,
∴AC⊥CD;
(3)∠BMC=45°.
如图,连接AD,
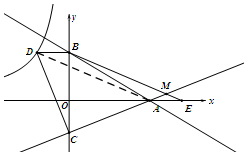
∵AE=OC,BD=OC,AE=BD,
∴BD∥x轴,
∴四边形AEBD为平行四边形,
∴AD∥BM,
∴∠BMC=∠DAC,
∵△OAC≌△BCD,
∴AC=CD,
∵AC⊥CD,
∴△ACD为等腰直角三角形,
∴∠BMC=∠DAC=45°.
(1)∵A(5,0),
∴OA=5.
∵tan∠OAC=
| 2 |
| 5 |
∴
| OC |
| OA |
| 2 |
| 5 |
∴C(0,-2),
∴BD=OC=2,
∵B(0,3),BD∥x轴,
∴D(-2,3),
∴m=-2×3=-6,
∴y=
| -6 |
| x |
设直线AC关系式为y=kx+b,
∵过A(5,0),C(0,-2),
∴
|
|
∴y=
| 2 |
| 5 |
(2)∵B(0,3),C(0,-2),
∴BC=5=OA,
在△OAC和△BCD中
|
∴△OAC≌△BCD(SAS),
∴AC=CD,
∴∠OAC=∠BCD,
∴∠BCD+∠BCA=∠OAC+∠BCA=90°,
∴AC⊥CD;
(3)∠BMC=45°.
如图,连接AD,

∵AE=OC,BD=OC,AE=BD,
∴BD∥x轴,
∴四边形AEBD为平行四边形,
∴AD∥BM,
∴∠BMC=∠DAC,
∵△OAC≌△BCD,
∴AC=CD,
∵AC⊥CD,
∴△ACD为等腰直角三角形,
∴∠BMC=∠DAC=45°.
看了 如图,已知点D在反比例函数y...的网友还看了以下:
平面解析几何1直线X*SinA-Y+1=0的倾斜角的变化范围是多少2已知圆O:X平方+Y平方=5和 2020-04-11 …
判断题..二次函数1.函数y=4x^2+5的图象可由y=4x^2的图象向左平移5个单位得到的2.y 2020-05-13 …
已知函数y=ax的平方+k的图像经过(1,3分之5)和(-3,-1)1.求函数的关系式,并指出顶点 2020-06-06 …
图1是对酶的某种特性的解释模型,图2、3、4、5、6、7是在不同条件下某种酶促反应的变化情况,据图 2020-07-11 …
钝角三角形一是等腰三角形()判断1.2.等腰三角形一定是等边三角形()3.有四条边组成的图形叫做四 2020-08-03 …
根据图画内容及所给提示,以peter,sSUnday为题写一篇60词左右的短文,介绍peter上周 2020-08-03 …
如图5-10-5所示,每级台阶的高度和宽度都是0.4m,一小球以水平速度v飞出,欲打在第四级台阶上, 2020-11-01 …
(1)将图中三角形绕点O顺时针旋转90°.(2)将旋转后的图形和向右平移5格.(3)把图中的三角形A 2020-11-03 …
(2014•莆田)如图为空气成分示意图.即将实施的《环境空气质量标准》中,农村地区PM2.5和PM1 2020-11-12 …
莫问桑田事,但看桑落洲。数家新住处,昔日大江流。古岸崩欲尽,平沙长未休。想应百年后,人世更悠悠。”读 2020-12-22 …