在正方形ABCD中，点P是射线CB上一个动点，连接PA，PD，点M、N分别为BC、AP的中点，连接MN交PD于点Q．（1）如图1，当点P与点B重合时，△QPM的形状是；（2）当点P在线段CB的延长线上时，如图2

Question

在正方形ABCD中，点P是射线CB上一个动点，连接PA，PD，点M、N分别为BC、AP的中点，连接MN交PD于点Q．
（1）如图1，当点P与点B重合时，△QPM的形状是___；
（2）当点P在线段CB的延长线上时，如图2．
①依题意补全图2；
②判断△QPM的形状并加以证明；
（3）点P′于点P关于直线AB对称，且点P′在线段BC上，连接AP′，若点Q恰好在直线AP′上，正方形ABCD的边长为2，请写出求此时BP长的思路（可以不写出计算结果）．

Answer 1

（1）如图1，连接AC，

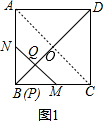
∵四边形ABCD为正方形，
∴AC⊥BD，∠DBC=45°，
∵点M、N分别为BC、AP的中点，
∴MN∥AC，
∴∠BQM=∠BOC=90°，
∴∠QMB=45°，
∴△QPM是等腰直角三角形，
故答案为：等腰直角三角形．
（2）①如图2，

②△QPM的形状是等腰三角形，
如图3，延长BC至E，使CE=BP，连接AE，

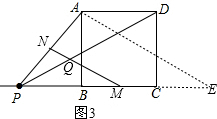
∵PB=CE，
∴PB+BC=CE+BC，即CP=BE，
∵四边形ABCD是正方形，
∴AB=DC，∠ABC=∠DCB=90°，
在△DCP和△ABE中，

DC=AB

∠DCP=∠ABE

CP=BE

∴△DCP≌△ABE，
∴∠DPC=∠E，
∵M为BC的中点，
∴MB=MC，
∴MB+BP=MC+CE，即MP=ME，
∴M为PE的中点，
∵N为AP的中点，
∴MN∥AE，
∴∠NMP=∠E，
∴∠DPC=∠NMP，
∴QM=QP，
∴△QPM是等腰三角形．
（3）求解思路如下：
a，由题意画出图形，并延长BC至E，使CE=BP，连接AE，如图4．

b，由（2）可得QM∥AE，可证(P′Q)/(QA)=(P′M)/(ME)．
c，由PP′∥AD，可证△P′PQ∽△ADQ，从而(P′Q)/(QA)=(P′P)/(AD)．
d，可得(P′M)/(ME)=(P′P)/(AD)．
e，由点P′与点P关于直线AB对称，得到BP′=BP=CE，设BP′=BP=CE=x，由AD=BC=2，可分别表示P′M，ME，P′P，可求BP的长．