已知正三角形ABC的三个顶点都在球心为O、半径为3的球面上，且三棱锥O-ABC的高为2，点D是线段BC的中点，过点D作球O的截面，则截面积的最小值为（）A.15π4B.4πC.7π2D.3π

Question

已知正三角形ABC的三个顶点都在球心为O、半径为3的球面上，且三棱锥O-ABC的高为2，点D是线段BC的中点，过点D作球O的截面，则截面积的最小值为（　　）

A.

(15π)/(4)

B. 4π

C.

(7π)/(2)

D. 3π

Answer 1

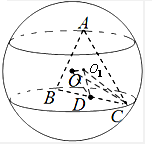设正△ABC的中心为O₁，连结O₁O、O₁C、O₁D、OD，
∵O₁是正△ABC的中心，A、B、C三点都在球面上，
∴O₁O⊥平面ABC，结合O₁C⊂平面ABC，可得O₁O⊥O₁C，
∵球的半径R=3，O₁O=2，
∴Rt△O₁OC中，O₁C=√(5)．
又∵D为BC的中点，∴Rt△O₁DC中，O₁D=(1)/(2)O₁C=(√(5))/(2)．
∴Rt△OO₁D中，OD=√(4+(5)/(4))=√((21)/(4))．
∵过D作球O的截面，当截面与OD垂直时，截面圆的半径最小，
∴当截面与OD垂直时，截面圆的面积有最小值．
此时截面圆的半径r=√(9-(21)/(4))=(√(15))/(2)，可得截面面积为S=πr²=(15π)/(4)．
故选A．