早教吧作业答案频道 -->数学-->
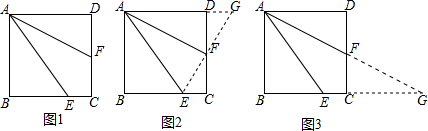
已知:如图1,在正方形ABCD,E是BC边上一点,F是CD的中点,且AE=DC+CE.求证:AF平分∠DAE.证法一:延长EF,交AD的延长线于G.(如图2)证法二:延长BC,交AF的延长线于G.(如图3)
题目详情
已知:如图1,在正方形ABCD,E是BC边上一点,F是CD的中点,且AE=DC+CE.求证:AF平分∠DAE.
证法一:延长EF,交AD的延长线于G.(如图2)
证法二:延长BC,交AF的延长线于G.(如图3)
证法一:延长EF,交AD的延长线于G.(如图2)
证法二:延长BC,交AF的延长线于G.(如图3)

▼优质解答
答案和解析
证明:证法一:
∵四边形ABCD是正方形,
∴AD=DC,∠ADC=∠C=90°,
∴∠FDG=90°,
∵F是CD的中点,
∴DF=CF,
在△ADF和△GCF中,
,
∴△ADF≌△GCF(ASA),
∴DG=CE,GF=EF,
∵AE=DC+CE,AG=AD+DG,
∴AE=AG,
∴AF平分∠DAE(三线合一).
证法二:
在△ADF和△GCF,
,
∴△ADF≌△GCF(ASA),
∴AD=CG,∠DAF=∠G,
∵EG=EC+CG,AE=AD+CE,
∴EG=AE,
∴∠FAE=∠G,
∴∠FAE=∠DAF,
即AF平分∠DAE.
∵四边形ABCD是正方形,
∴AD=DC,∠ADC=∠C=90°,
∴∠FDG=90°,
∵F是CD的中点,
∴DF=CF,
在△ADF和△GCF中,
|
∴△ADF≌△GCF(ASA),
∴DG=CE,GF=EF,
∵AE=DC+CE,AG=AD+DG,
∴AE=AG,
∴AF平分∠DAE(三线合一).
证法二:
在△ADF和△GCF,
|
∴△ADF≌△GCF(ASA),
∴AD=CG,∠DAF=∠G,
∵EG=EC+CG,AE=AD+CE,
∴EG=AE,
∴∠FAE=∠G,
∴∠FAE=∠DAF,
即AF平分∠DAE.
看了 已知:如图1,在正方形ABC...的网友还看了以下:
在图3中,E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点,并且图中阴影部分 2020-05-16 …
(2013•济南二模)图甲为人的膝跳反射示意图,图乙为图甲中结构d的放大图,据图回答下列有关问题. 2020-06-28 …
请据图回答:(1)图2中e点与d点相比较,e点时叶肉细胞中C3的含量;e点与f点相比较,e点时叶肉 2020-07-09 …
(9分)请据图回答:(1)图2中e点与d点相比较,e点时叶肉细胞中C3的含量;e点与f点相比较,e 2020-07-09 …
如图a所示是小明设计的电子秤原理图,其中E为由两节干电池串联组成的电源,v是电压表,R0是阻值为5 2020-07-12 …
如图1,若AB∥CD,则有∠B+∠D=∠E.1.将点E移至图2的位置时,∠D,∠B,∠E有什么关系 2020-07-20 …
如图1为溴原子(Br)的结构示意图;如图2为A、B、C、D、E5种粒子的结构示意图.请回答下列问题 2020-07-24 …
读下列两幅美洲图回答问题(1)在图一中E是海峡,B是洋,D是岛,数字①是山脉,此山脉属于山系的一部分 2020-11-27 …
已知:如图1,图形①满足AD=AB,MD=MB,∠A=72°,∠M=144°。图形②与图形①恰好拼成 2020-12-23 …
(14分)读图,(其中图乙为图甲中虚线方框区域)完成下列问题。(1)图甲中E河流域的聚落主要分布在什 2020-12-24 …