早教吧作业答案频道 -->数学-->
已知平行四边形ABCD中,(1)如图1,若DE=BF,求证:四边形AFCE是平行四边形;(2)若AE、CF分别是∠DAB,∠BCD的平分线,求证:四边形AFCE是平行四边形;(3)如图2,在(1)的基础上,连接B
题目详情
已知平行四边形ABCD中,
(1)如图1,若DE=BF,求证:四边形AFCE是平行四边形;
(2)若AE、CF分别是∠DAB,∠BCD的平分线,求证:四边形AFCE是平行四边形;
(3)如图2,在(1)的基础上,连接BE,DF,分别交FC,EA于点G,H.求证:四边形EHFG为平行四边形.
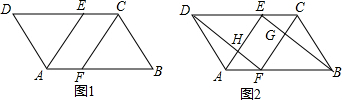
(1)如图1,若DE=BF,求证:四边形AFCE是平行四边形;
(2)若AE、CF分别是∠DAB,∠BCD的平分线,求证:四边形AFCE是平行四边形;
(3)如图2,在(1)的基础上,连接BE,DF,分别交FC,EA于点G,H.求证:四边形EHFG为平行四边形.

▼优质解答
答案和解析
(1)证明:∵四边形ABCD为平行四边形,
∴AB=CD.AB∥CD,
又∵DE=BF,
∴AB-BF=CD-DE.即AF=CE,
∴四边形AFCE是平行四边形.
(2)证明:∵四边形ABCD是平行四边形,
∴∠DAB=∠BCD,AB∥CD,
∴∠BAE=∠DEA,
∵AE、CF分别是∠DAB,∠BCD的平分线,
∴∠BAE=∠DCF,
∴∠DEA=∠DCF,
∴AE∥CF,
∴四边形AFCE是平行四边形.
(3)证明:由(1)得:四边形AFCE是平行四边形,
∴AF=CE,AE∥CF,
∵AB=CD,
∴BF=DE,
又∵AB∥CD,
∴四边形BEDF为平行四边形,
∴DF∥BE,
∴四边形EHFG为平行四边形.
∴AB=CD.AB∥CD,
又∵DE=BF,
∴AB-BF=CD-DE.即AF=CE,
∴四边形AFCE是平行四边形.
(2)证明:∵四边形ABCD是平行四边形,
∴∠DAB=∠BCD,AB∥CD,
∴∠BAE=∠DEA,
∵AE、CF分别是∠DAB,∠BCD的平分线,
∴∠BAE=∠DCF,
∴∠DEA=∠DCF,
∴AE∥CF,
∴四边形AFCE是平行四边形.
(3)证明:由(1)得:四边形AFCE是平行四边形,
∴AF=CE,AE∥CF,
∵AB=CD,
∴BF=DE,
又∵AB∥CD,
∴四边形BEDF为平行四边形,
∴DF∥BE,
∴四边形EHFG为平行四边形.
看了 已知平行四边形ABCD中,(...的网友还看了以下:
填单词使横竖六行成单词第一行()()e第二行()e()第三行()e() 2020-04-26 …
小常识-变频调速为什么缩写为VVVF?VVVF的意思是"变压变频".交流异步电动机在运行时,外加电 2020-05-14 …
高二物理动量基础应用题(只要答案)一颗二战苏联产手榴弹在5m高处以Vo=10m/s的速度水平飞行时 2020-05-22 …
如图,AB平行CD,AB交平面a=B,CD交平面a=D,AC交平面a=E. 2020-06-12 …
P是矩形ABCD所在平面外一点,PA垂直平面ABCD,E.F分别是AB,PD的中点,又二面角为45 2020-06-21 …
如图,cd为三角形ABC的角平分线,e、f分别在cd、bd上且da等于df,ef等于ac,求证e平 2020-06-28 …
所示在三角形ABC中,E,F分别为AB,AC边上的一点,EF平行于BC,将线段EB平移,使E点移到 2020-07-09 …
设a是任意向量,e是一单位向量,且a平行e,则下列表达中正确的是Ae=a/|a|Ba=|a|eCa 2020-07-30 …
关于下面图形中四条线段的关系,有下面几种说法,其中正确的是A.a和b互相垂直B.b和c互相垂直C. 2020-08-02 …
求函数y=(e的x次方减a)的平方+(e的-x次方减a)的平方(a大于0小于2)的最小值求函数y=( 2020-12-08 …