某沿海城市的海边有两条相互垂直的直线型公路l1、l2，海岸边界MPN近似地看成一条曲线段．为开发旅游资源，需修建一条连接两条公路的直线型观光大道AB，且直线AB与曲线MPN有且仅有一个

Question

某沿海城市的海边有两条相互垂直的直线型公路l₁、l₂，海岸边界MPN近似地看成一条曲线段．为开发旅游资源，需修建一条连接两条公路的直线型观光大道AB，且直线AB与曲线MPN有且仅有一个公共点P（即直线与曲线相切），如图所示．若曲线段MPN是函数y=(a)/(x)图象的一段，点M到l₁、l₂的距离分别为8千米和1千米，点N到l₂的距离为10千米，以l₁、l₂分别为x、y轴建立如图所示的平面直角坐标系xOy，设点P的横坐标为p．

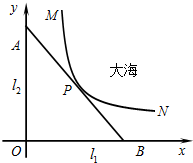
（1）求曲线段MPN的函数关系式，并指出其定义域；
（2）若某人从点O沿公路至点P观景，要使得沿折线OAP比沿折线OBP的路程更近，求p的取值范围．

Answer 1

（1）由题意得M（1，8），则a=8，故曲线段MPN的函数关系式为y=(8)/(x)，（4分）
又得N(10，(4)/(5))，所以定义域为[1，10]．…（6分）
（2）P(p，(8)/(p))，设AB：y-(8)/(p)=k(x-p)
由

y-(8)/(p)=k(x-p)

y=(8)/(x)

得kpx²+（8-kp²）x-8p=0，
△=（8-kp²）²+32kp²=（kp²+8）²=0，…（8分）
∴kp²+8=0，∴k=-(8)/(p2)，得直线AB方程为y-(8)/(p)=-(8)/(p2)(x-p)，…（10分）
得A(0，(16)/(p))、B(2p，0)，故点P为AB线段的中点，
由2p-(16)/(p)=2•(p2-8)/(p)>0即p²-8>0…（12分）
得p>2√(2)时，OA<OB，
所以，当2√(2)<p≤10时，经点A至P路程最近．（14分）