早教吧作业答案频道 -->数学-->
如图1,在△ABC中,BC=4,以线段AB为边作△ABD,使得AD=BD,连接DC,再以DC为边作△CDE,使得DC=DE,∠CDE=∠ADB=α.(1)如图2,当∠ABC=45°且α=90°时,用等式表示线段AD,DE之间的数量关系;(2
题目详情
如图1,在△ABC中,BC=4,以线段AB为边作△ABD,使得AD=BD,连接DC,再以DC为边作△CDE,使得DC=DE,∠CDE=∠ADB=α.
(1)如图2,当∠ABC=45°且α=90°时,用等式表示线段AD,DE之间的数量关系;
(2)将线段CB沿着射线CE的方向平移,得到线段EF,连接BF,AF.
①若α=90°,依题意补全图3,求线段AF的长;
②请直接写出线段AF的长(用含α的式子表示).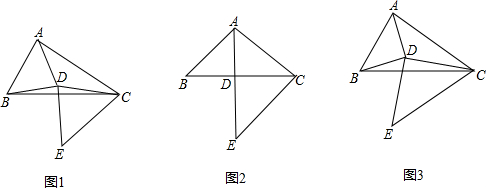
(1)如图2,当∠ABC=45°且α=90°时,用等式表示线段AD,DE之间的数量关系;
(2)将线段CB沿着射线CE的方向平移,得到线段EF,连接BF,AF.
①若α=90°,依题意补全图3,求线段AF的长;
②请直接写出线段AF的长(用含α的式子表示).

▼优质解答
答案和解析
(1)AD+DE=4,
理由是:如图1,
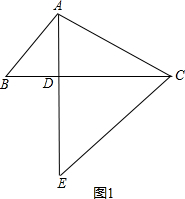
∵∠ADB=∠EDC=∠α=90°,AD=BD,DC=DE,
∴AD+DE=BC=4;
(2)①补全图形,如图2,
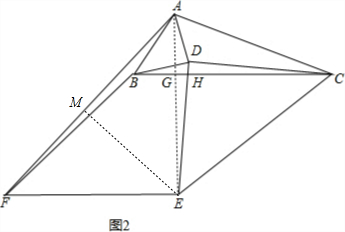
设DE与BC相交于点H,连接AE,
交BC于点G,
∵∠ADB=∠CDE=90°,
∴∠ADE=∠BDC,
在△ADE与△BDC中,
,
∴△ADE≌△BDC,
∴AE=BC,∠AED=∠BCD.
∵DE与BC相交于点H,
∴∠GHE=∠DHC,
∴∠EGH=∠EDC=90°,
∵线段CB沿着射线CE的方向平移,得到线段EF,
∴EF=CB=4,EF∥CB,
∴AE=EF,
∵CB∥EF,
∴∠AEF=∠EGH=90°,
∵AE=EF,∠AEF=90°,
∴∠AFE=45°,
∴AF=
=4
;
②如图2,过E作EM⊥AF于M,
∵由①知:AE=EF=BC,
∴∠AEM=∠FEM=
,AM=FM,
∴AF=2FM=EF×sin
=8sin
.
理由是:如图1,

∵∠ADB=∠EDC=∠α=90°,AD=BD,DC=DE,
∴AD+DE=BC=4;
(2)①补全图形,如图2,

设DE与BC相交于点H,连接AE,
交BC于点G,
∵∠ADB=∠CDE=90°,
∴∠ADE=∠BDC,
在△ADE与△BDC中,
|
∴△ADE≌△BDC,
∴AE=BC,∠AED=∠BCD.
∵DE与BC相交于点H,
∴∠GHE=∠DHC,
∴∠EGH=∠EDC=90°,
∵线段CB沿着射线CE的方向平移,得到线段EF,
∴EF=CB=4,EF∥CB,
∴AE=EF,
∵CB∥EF,
∴∠AEF=∠EGH=90°,
∵AE=EF,∠AEF=90°,
∴∠AFE=45°,
∴AF=
| EF |
| cos45° |
| 2 |
②如图2,过E作EM⊥AF于M,
∵由①知:AE=EF=BC,
∴∠AEM=∠FEM=
| α |
| 2 |
∴AF=2FM=EF×sin
| α |
| 2 |
| α |
| 2 |
看了 如图1,在△ABC中,BC=...的网友还看了以下:
设函数f(x)=x^2-alnx与g(x)=(1/a)x-根号x的图像分别交直线x=1于点A,B, 2020-04-05 …
某中学图书馆计划购买近期畅销的3、B两种图书各若干本,其中3种图书单价为43元/本,B种图书单价为 2020-04-06 …
如图,A是反比例函数y=x分之k的图象上的一点AB⊥x轴于点B,且△ABO的面积是1.5,则k的值 2020-04-08 …
1在平面直角坐标系XOY中,已知一次函数Y=KX+B(K不等于0)的图像经过点P(1.1),与X轴 2020-05-13 …
已知反比例函数y=k/x的图象经A(-根号3,m)过点A作AB垂直于X轴于点B且三角形的面积为根号 2020-05-15 …
函数数学题.设f(x)=x^2-alnx g(x)=x-a根号x的图像分别交直线x+1于点A,B, 2020-05-15 …
如图,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且 ,G是EF的中点.求二面角 2020-05-16 …
如图,已知直线a‖b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为如图,已 2020-05-16 …
在反比例函数y=x分之8(x>0)的图像上有两点A,B,且点A的纵坐标为2,点B的横坐标为2在反比 2020-06-14 …
如图所示已知AD与AB、CD交于A、D俩点,EC、BF与AB、CD相交于点E、C、B、F,且∠1= 2020-06-27 …